The straight lines y=±x intersect the parabola y2=8x in points P and Q, then length of PQ is
4
4√2
8
16
The correct Answer is:D
We have, y2=8x
∴y2=±8y [∵x=±y]
⇒y2−+8y=0⇒y(y±8)=0
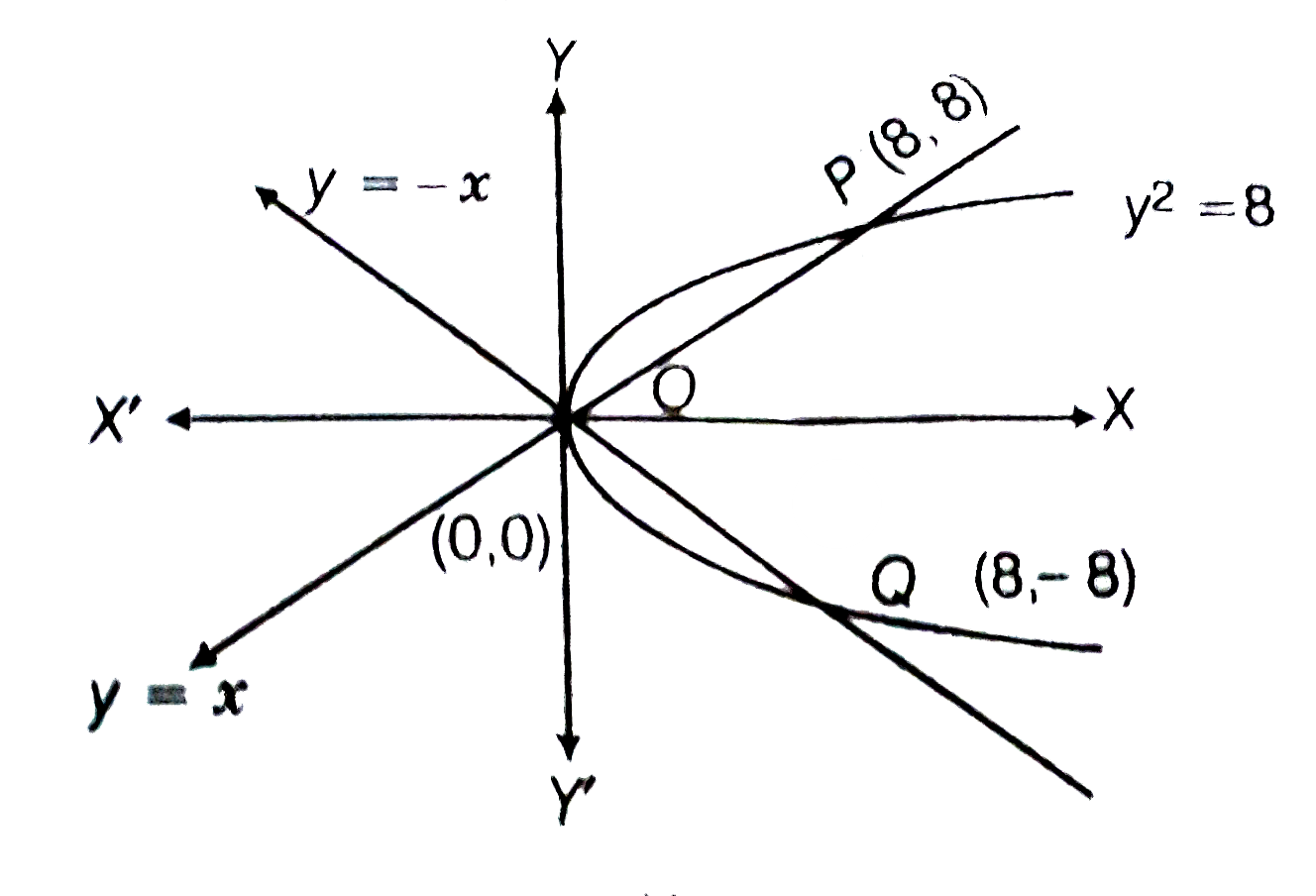
⇒y=0,±8
∴P(8.8),Q=(8,−8)
∴ Length of PQ=√(16)2+(0)2=16
Topper's Solved these Questions
Similar Questions
Knowledge Check
The line 4x−7y+10=0 intersects the parabola y2=4x at the points P and Q. The coordinates of the point of intersection of the tangents drawn at the points P and Q are
A(−72,−52)B(52,72)C(−52,−72)D(72,52)The straight line x+y=a touches the parabola y=x−x2 If a =
A0B1C-1Dnone
If the line x−y−1=0 intersect the parabola y2=8x at P and Q, then find the point on intersection of tangents PandQ.
View SolutionStatement 1: If the straight line x=8 meets the parabola y2=8x at PandQ, then PQ substends a right angle at the origin. Statement 2: Double ordinate equal to twice of latus rectum of a parabola subtends a right angle at the vertex.
View SolutionIf the straight line 4y-3x+18=0 cuts the parabola y2=64x in P&Q then the angle subtended by PQ at the vertex of the parabola is
View SolutionThe line y=x−2 cuts the parabola y2=8x in the points A and B. The normals drawn to the parabola at A and B intersect at G. A line passing through G intersects the parabola at right angles at the point C, and the tangents at A and B intersect at point T.
View SolutionTangents are drawn from the point(-1, 2) to the parabola y2=4x. These tangents meet the line x=2 at P and Q, then length of PQ is
View SolutionThe line 2x−y+4=0 cuts the parabola y2=8x in PandQ. The mid-point of PQ is (a) (1,2) (b) (1,−2) (c) (−1,2) (d) (−1,−2)
View Solution
