The triangle formed by the tangent to the curve f(x)=x2+bx−b at the point (1,1) and the coordinate axes, lies in the first quadrant. If its area is 2, then the value of b is (a) −1 (b) 3 (c) −3 (d) 1
−1
−52
−3
1
The correct Answer is:C
Since, tangent at (1,1) to the parabola forms a triangle with axis, which lie in the first quadrant, vertex lies to the ringt of x=1.
∴−b2>1⇒b<−2
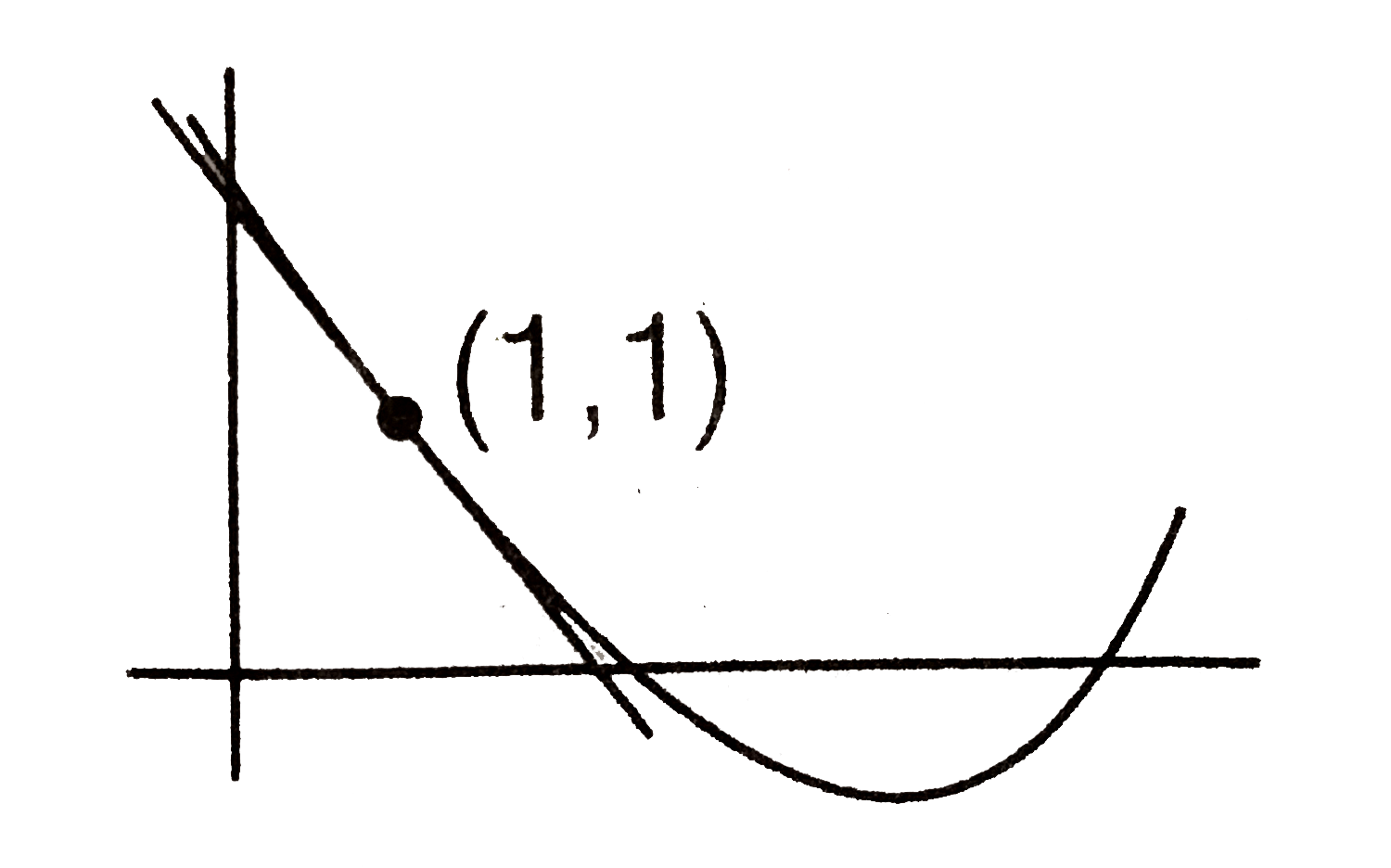
Equation of tangent at (1,1) is
y−1=(b+2)(x−1)
∴x-intercept=(b+1)b+2
y-intercept=-(b+1)
∴ Area of Δ=−(b+1)22(b+2)=2
⇒b2+6b+9=0
⇒b=−3.
Topper's Solved these Questions
Similar Questions
The triangle formed by the tangent to the curve f(x)=x2+bx−b the point (1, 1) and the co-ordinate axes, lies in the first quadrant. If its area is 2, then the value of b is
View SolutionIf the area of the triangle formed by a tangent to the curve xny=an+1 and the coordinate axes is constant, then n=
View Solution
Knowledge Check
The triangle formed by the normal to the curve f(x)=x2−ax+2a at the point (2,4) and the coordinate axes lies in second quadrant, if its area is 2 sq units, then a can be
A2B17/4C5DNone of theseThe area of the triangle formed by the tangent at the point (a, b) to the circle x2+y2=r2 and the coordinate axes, is
Ar42abBr42|ab|Cr4abDr4|ab|The area of the traingle formed by the coordinate axes and a tangent to the curve xy=a2 at the point (x1,y1) is
Aa2x1y1Ba2y1x1C2a2D4a2
The minimum area of triangle formed by any tangent to the ellipse x2a2+y2b2=1 with the coordinate axes, is
View SolutionThe muinimum area of the triangle formed by the tangent to x2a2+y2b2=1 and the coordinate axes is
View SolutionThe muinimum area of the triangle formed by the tangent to x2a2+y2b2=1 and the coordinate axes is
View SolutionThe muinimum area of the triangle formed by the tangent to x2a2+y2b2=1 and the coordinate axes is
View SolutionThe minimum area (sq. units) of triangle formed by the tangent to the x2a2+y2b2=1 and coordinate axes is:
View Solution
