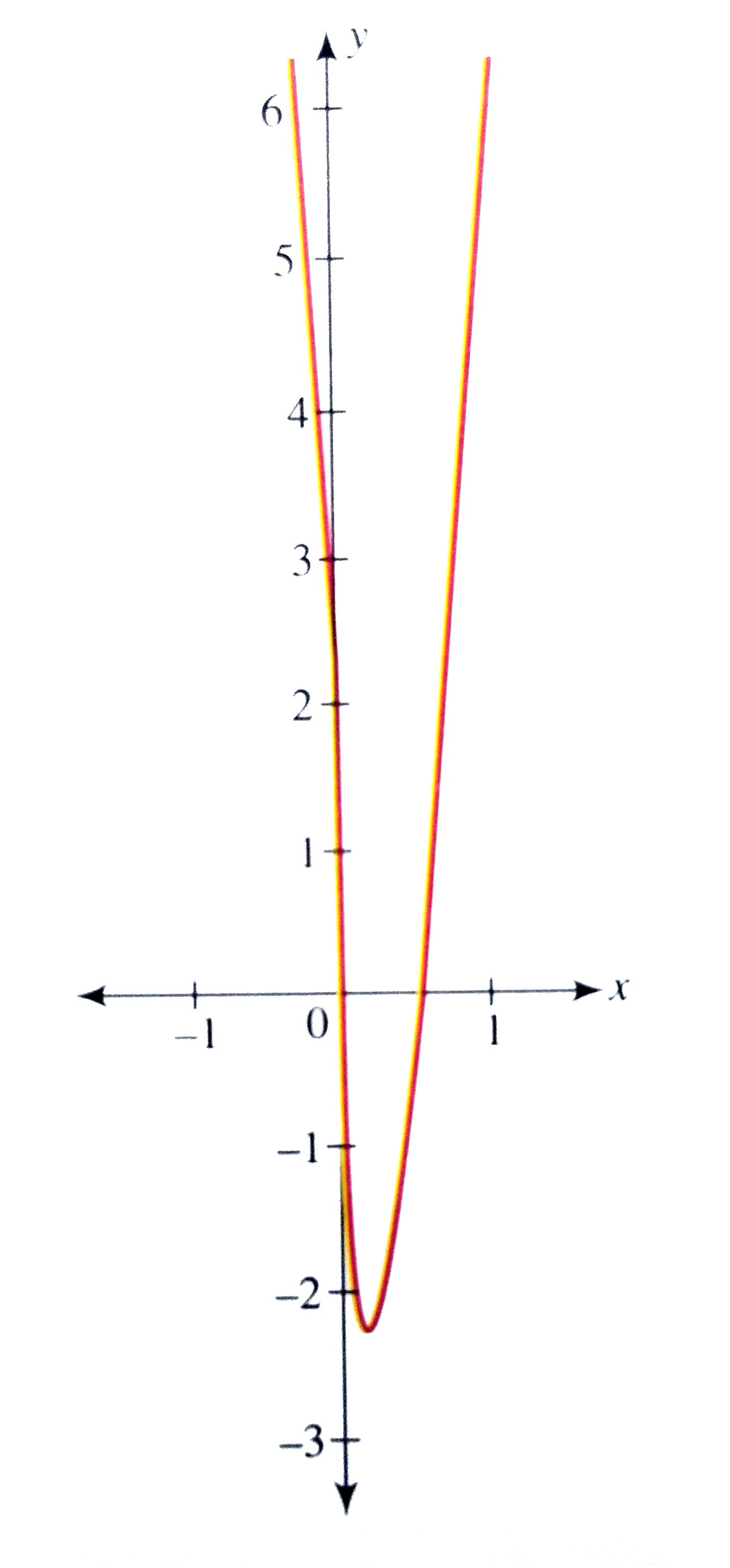
Draw the graph of f(x)=12x43−6x13Solution in Tamil
We have y=f(x)=12x43−6x13
Clearly, the domain of the function is R.
f(x)=0∴12x43−6x13=0
or 6x13(2x−1)=0
or x=0,x=1/2
So the curve meets the x-axis at (0,0) and (1/2,0).
Now, f′(x)=16x13−2x−23=2(8x−1)x23
f′(x)<0 for x<18, where f(x) decreases.
So, x=1/8 is the point of minima.
Also the function is non-differentianble at x=0, as f(x) has a vertical tangent at (0,0). Therefore, the graph of the function is as shown in the following figure.
Topper's Solved these Questions
Similar Questions
Draw the graph of y=sin2x−cosx
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionSolve: (x+2)3=2x(x2−1)
View SolutionFind absolute maximum and minimum values of a function f given by f(x)=12x43−6x13,x∈[−1,1].
View SolutionIf f(x)=x9−6x8−2x7+12x6+x4−7x3+6x2+x−3, find f(6).
View SolutionFind absolute maximum and minimum values of a function f given by f(x)=12x4/3−6x1/3, x∈[−1, 1] .
View SolutionIf f(x)=x9−6x8−2x7+12x6+x4−7x3+6x2+x−3, find f(6).
View SolutionShow that f(x) =(x3−6x2+12x−8) does not have any point of local maxima or minima . Hence draw graph
View SolutionDraw the graph of f(x)=12x43−6x13
View SolutionIf x=21/3−2, then x3+6x2+12x=_______
View Solutionf(x)=12x4/3−6x1/3,x∈[−1,1] द्वारा प्रदत एक फलन f के निरपेक्ष उच्तम और निरपेक्ष मान ज्ञात कीजिए।
View SolutionFind absolute maximum and minimum values of a function f given by
f(x)=12x43−6x13,x∈[−01,1]
View SolutionFind absolute maximum and minimum values of a function f given by
f(x)=12x43−6x13,x∈[−01,1]
View SolutionFind absolute maximum and minimum values of a function f given by
f(x) =12x^((4)/(3))-6x^((1)/(3)),x in [-1,1]
View SolutionAn equation of tangent line at an inflection point of f(x)=x4−6x3+12x2−8x+3 is
View SolutionDraw the graph of f(x)=12x43−6x13
View Solution
