Question

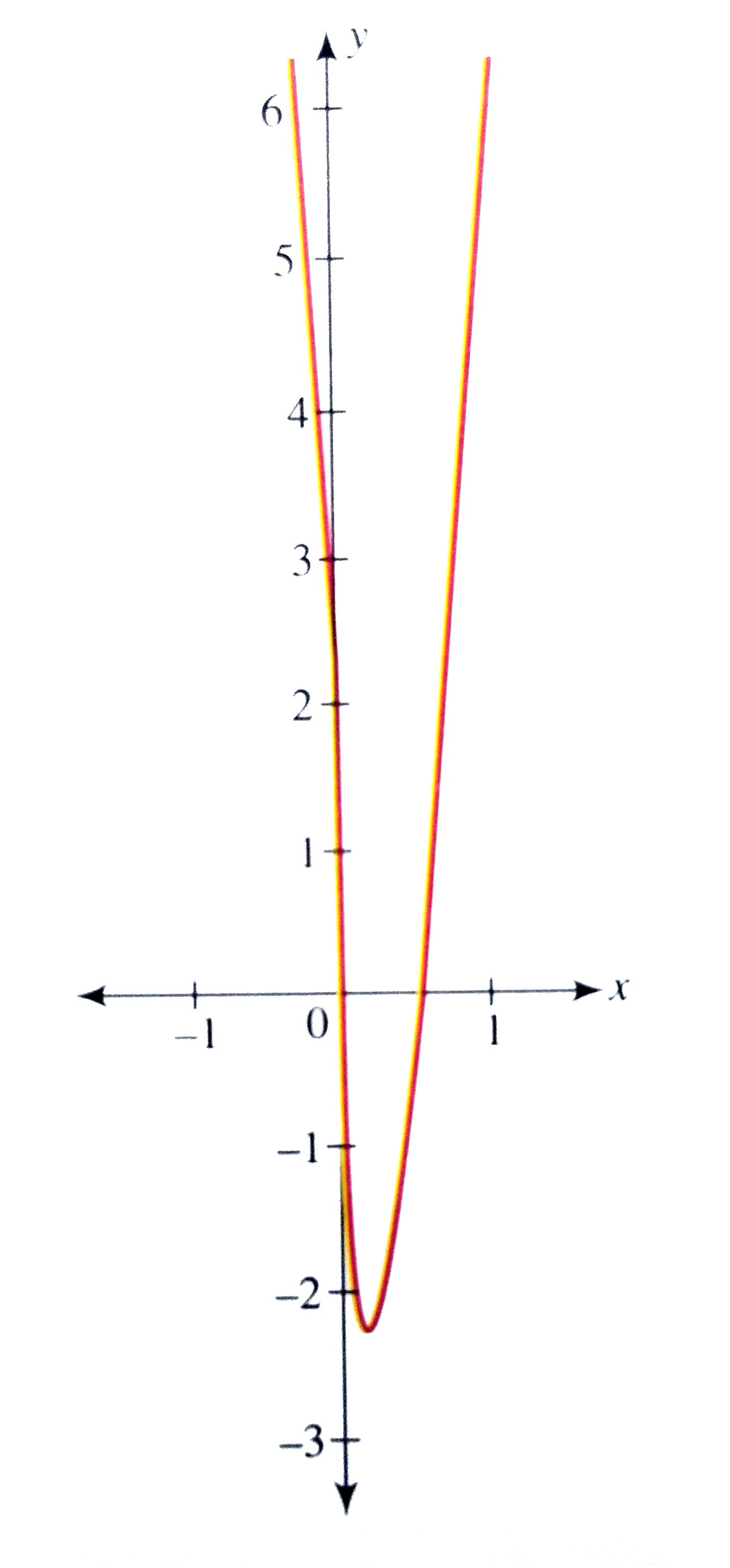
Draw the graph of $f\left(x\right)=12x^{\frac{4}{3}}-6x^{\frac{1}{3}}$

Explanation

We have `y=f(x)=12x^(4/3)-6x^(1/3)`
Clearly, the domain of the function is R.
`f(x)=0 therefore 12x^(4/3)-6x^(1/3)=0`
or `6x^(1/3)(2x-1) =0`
or `x=0, x=1//2`
So the curve meets the x-axis at (0,0) and `(1//2,0)`.
Now, `f^(')(x) = 16x^(1/3)-2x^(-2/3) = (2(8x-1))/(x^(2/3))`
`f^(')(x) lt 0` for `x lt 1/8`, where `f(x)` decreases.
So, `x=1//8` is the point of minima.
Also the function is non-differentianble at `x=0`, as f(x) has a vertical tangent at (0,0). Therefore, the graph of the function is as shown in the following figure.