If the area bounded by f(x)=√tanx,y=f(c),x=0andx=a,0<c<a<π2 is minimum then find the value of c.Solution in Tamil
Graph of f(x)=√tanx is as shown in the following figure.
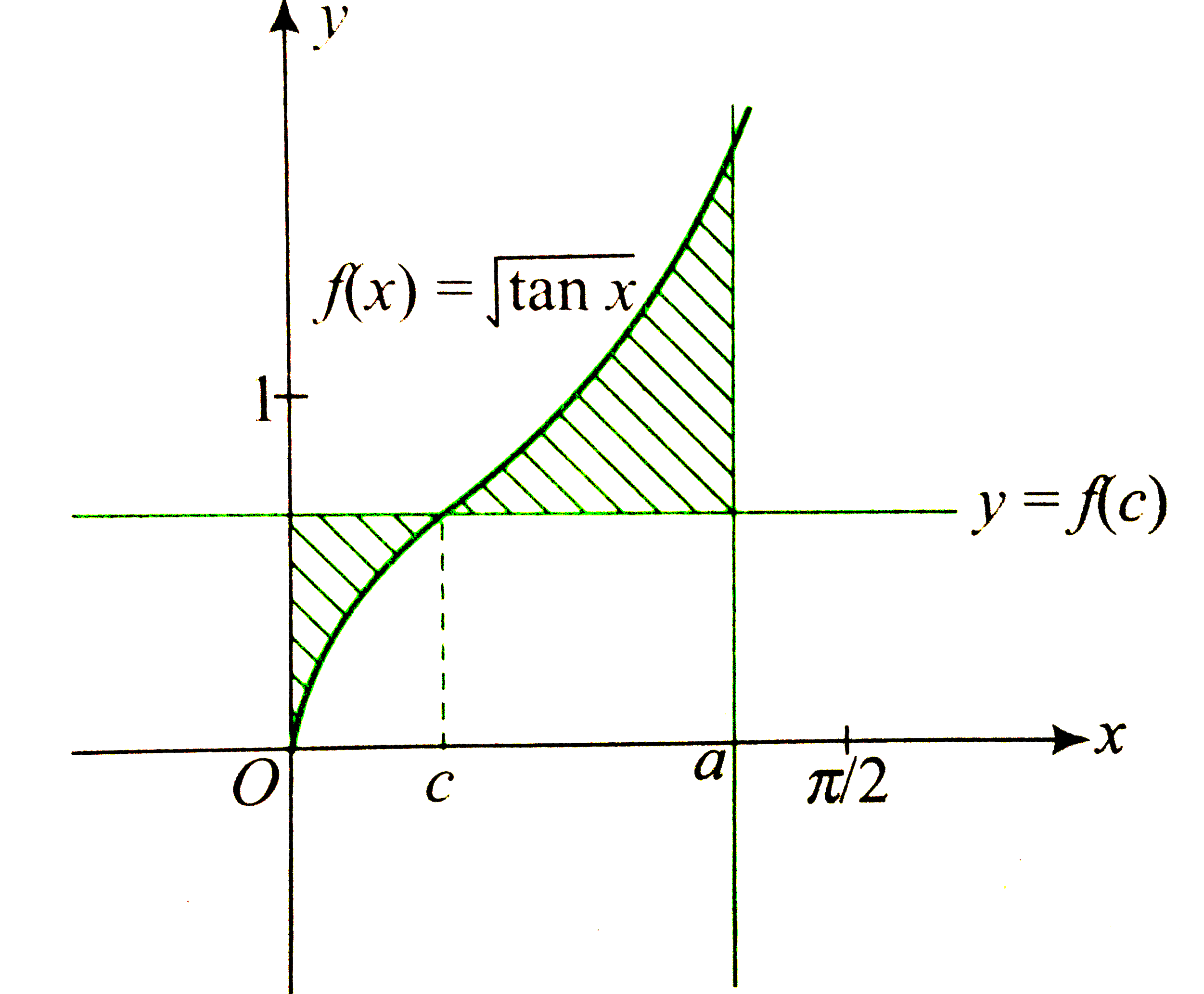
Required area is
A=c∫0(f(c)−f(x))dx+a∫c(f(x)−f(c))dx
=c∫0√tancdx−c∫0√tanxdx+a∫c√tanxdx−a∫c√tancdx
=(2c−a)√tanc−c∫0√tanxdx+a∫c√tanxdx
∴ dAdc=2√tanc+(2c−a)sec2c2√tanc−√tanc−√tanc
=(2c−a)sec2c2√tanc
dAdc=0⇒c=a2
At c=a2,dAdc changes sign from negative to positive
Hence A is minimum when c=a2
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionIf area bounded by f(x)=sin(x^(2)) with x axis,from x=0 to x=sqrt((pi)/(2)) is A,then
View SolutionFor what values of a∈[0,1] does the area of the fiqure bounded by the graph of the function y=f(x) and the straight lines x=0x=1&y=f(a) is at a minimum & for what values it is at a maximum if f(x)=√1−x2 Find also the maximum & the minimum areas.
View SolutionLet f(x)= minimum (x+1,sqrt(1-x) for all x<=1 then the area bounded by y=f(x) and the x -axis,is
View SolutionIf the area bounded by f(x)=√tanx,y=f(c),x=0andx=a,0<c<a<π2 is minimum then find the value of c.
View SolutionThe area bounded by the graph of y=f(x),f(x)>0 on [0,a] and x-axis is a22+a2sina+π2cosa then find the value of f(π2).
View SolutionLet f(x) = minimum (x+1,√1−x) for all x≤1. Then the area bounded by y=f(x) and the x−axis is
View SolutionIf f'(x)=tan−1(Secx+tanx),x∈(−π2,π2) and f(0)=0 then the value of f(1) is
View SolutionLet f(x) = minimum (tan x, cot x, 1/√3) ∀x∈[0,π/2] . Then area bounded by y = f(x) and the x-axis is log (ab)+πc√d, then a + b - c + d = _______
View SolutionLet f(x) = minimum (tan x, cot x, 1/√3) ∀×∈[0,π/2]. Then area of bounded by y = f(x) and the x-axis is in (43)+πk√3, then the value of k is ______
View SolutionIf the area bounded by f(x)=√tanx,y=f(c),x=0andx=a,0<c<a<π2 is minimum then find the value of c.
View SolutionThe area bounded by the graph of y=f(x),f(x)>0 on [0,a] and x-axis is a22+a2sina+π2cosa then find the value of f(π2).
View Solution
