If the area bounded by $f (x) = \sqrt{tan x}, y = f (c), x = 0 and x = a, 0 < c < a < \frac{π}{2}$ is minimum then find the value of c.

Video Solution

Text Solution

Verified by Experts

Graph of $f (x) = \sqrt{tan x}$ is as shown in the following figure.

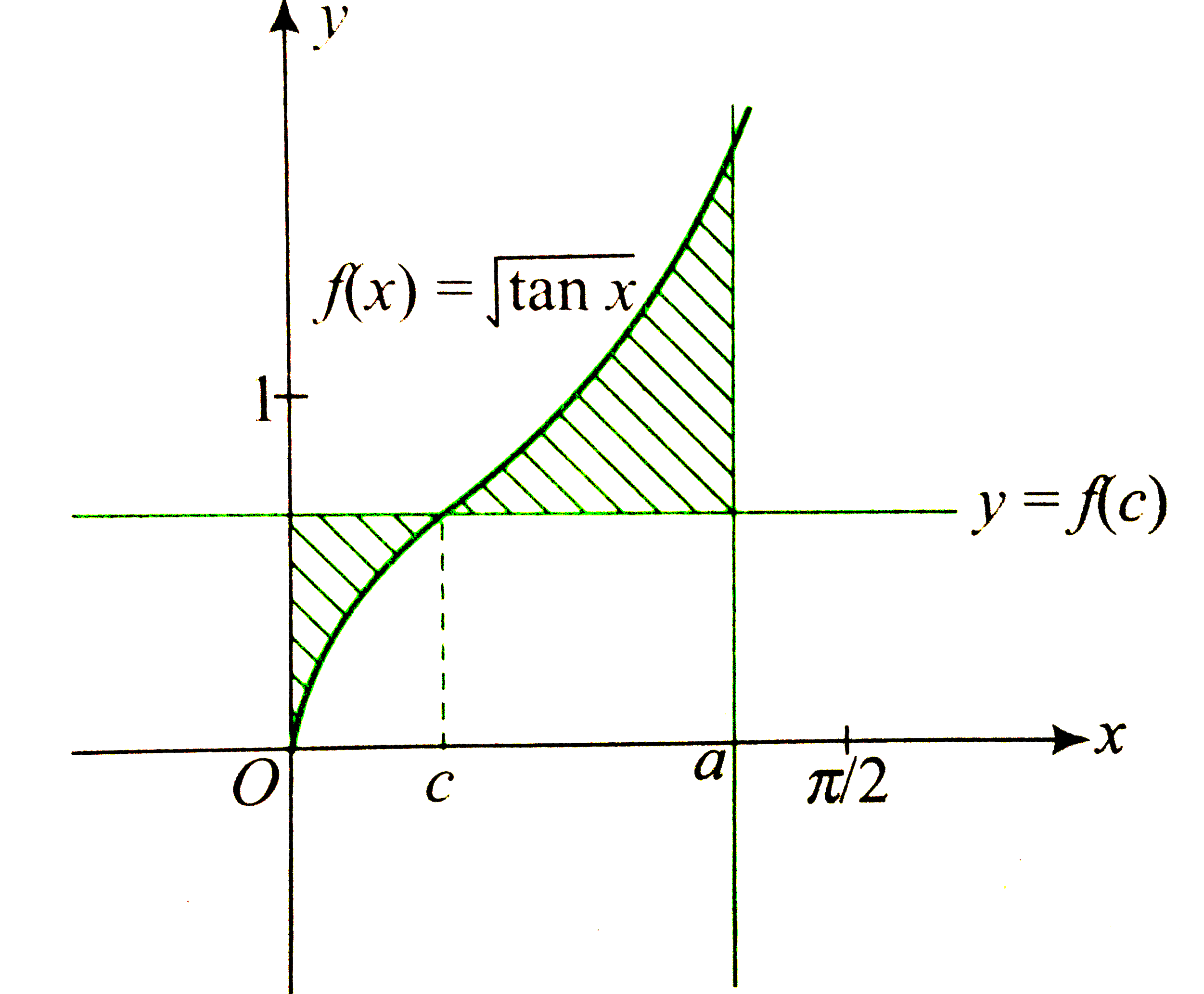
Required area is
$A = c \int 0 (f (c) - f (x)) d x + a \int c (f (x) - f (c)) d x$
$= c \int 0 \sqrt{tan c} d x - c \int 0 \sqrt{tan x} d x + a \int c \sqrt{tan x} d x - a \int c \sqrt{tan c} d x$
$= (2 c - a) \sqrt{tan c} - c \int 0 \sqrt{tan x} d x + a \int c \sqrt{tan x} d x$
$∴ \frac{d A}{d c} = 2 \sqrt{tan c} + (2 c - a) \frac{{sec}^{2} c}{2 \sqrt{tan c}} - \sqrt{tan c} - \sqrt{tan c}$
$= (2 c - a) \frac{{sec}^{2} c}{2 \sqrt{tan c}}$
$\frac{d A}{d c} = 0 \Rightarrow c = \frac{a}{2}$
$At c = \frac{a}{2}, \frac{d A}{d c}$ changes sign from negative to positive
Hence A is minimum when $c = \frac{a}{2}$

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at $x = a, x = b, y = f (x) and y = f (c) (where c \in (a, b)) is minimum when c = \frac{a + b}{2}$ .
$Proof : A = \int_{a}^{c} (f (c) - f (x)) d x + \int_{c}^{b} (f (c)) d x$
$= f (c) (c - a) - \int_{a}^{c} (f (x)) d x + \int_{a}^{b} (f (x)) d x - f (c) (b - c)$
$\Rightarrow A = [2 c - (a + b)] f (c) + \int_{c}^{b} (f (x)) d x - \int_{a}^{c} (f (x)) d x$

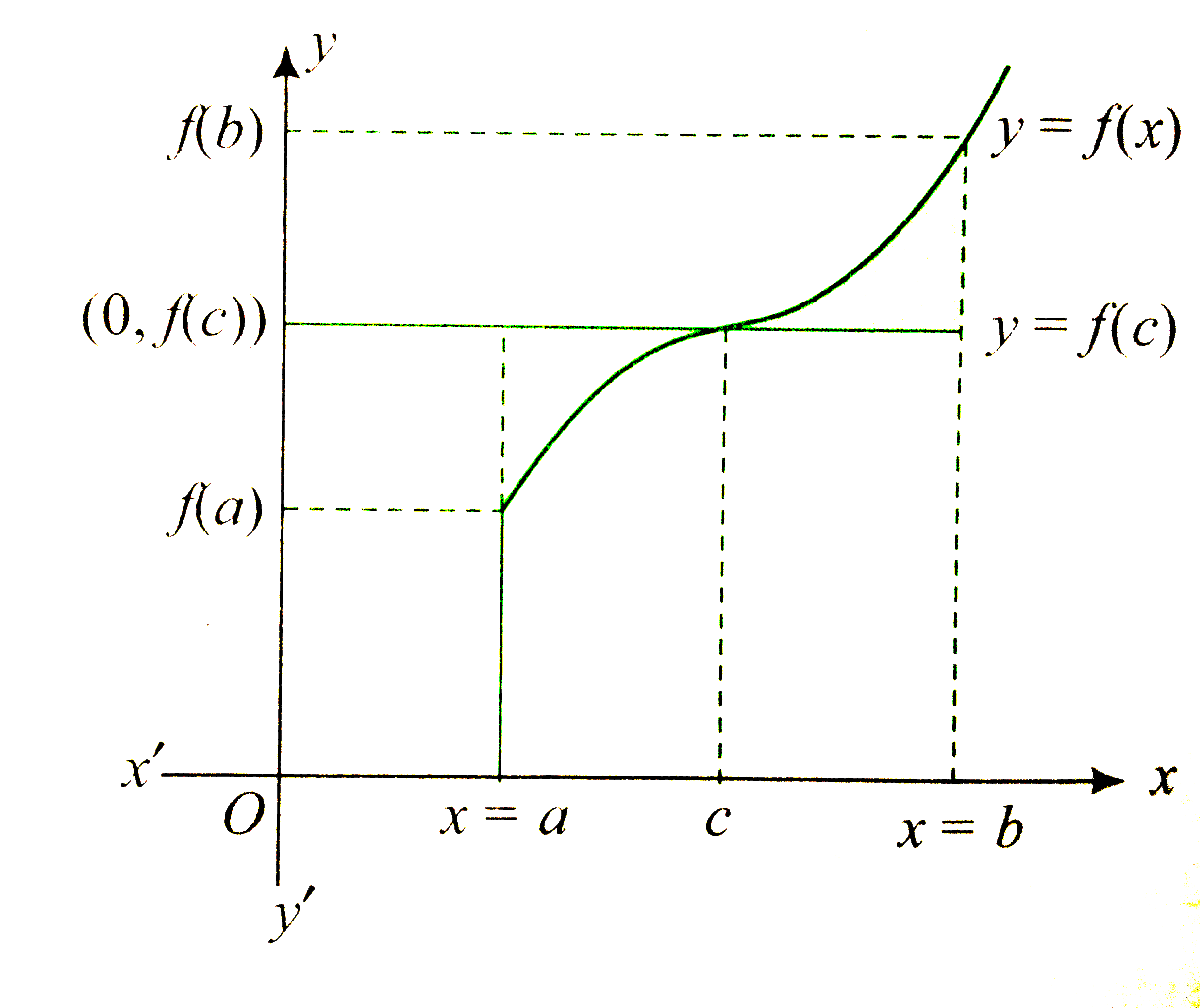
Differentiating w.r.t. c, we get
$\frac{d A}{d c} = [2 c - (a + b)] f' (c) + 2 f (c) + 0 - f (c) - (f (c) - 0)$
For maxima and minima , $\frac{d A}{d c} = 0$
$\Rightarrow f' (c) [2 c - (a + b)] = 0 (a s f' (c) \neq 0)$
Hence, $c = \frac{a + b}{2}$
$Also for c < \frac{a + b}{2}, \frac{d A}{d c} < 0 and for c > \frac{a + b}{2}, \frac{d A}{d c} > 0$
Hence, A is minimum when $c = \frac{a + b}{2}$ .
If the area bounded by $f (x) = \frac{x^{3}}{3} - x^{2} + a$ and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is
A $1 / 2$
B2
C1
D $2 / 3$
Question 2 - Select One
If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at $x = a, x = b, y = f (x) and y = f (c) (where c \in (a, b)) is minimum when c = \frac{a + b}{2}$ .
$Proof : A = \int_{a}^{c} (f (c) - f (x)) d x + \int_{c}^{b} (f (c)) d x$
$= f (c) (c - a) - \int_{a}^{c} (f (x)) d x + \int_{a}^{b} (f (x)) d x - f (c) (b - c)$
$\Rightarrow A = [2 c - (a + b)] f (c) + \int_{c}^{b} (f (x)) d x - \int_{a}^{c} (f (x)) d x$

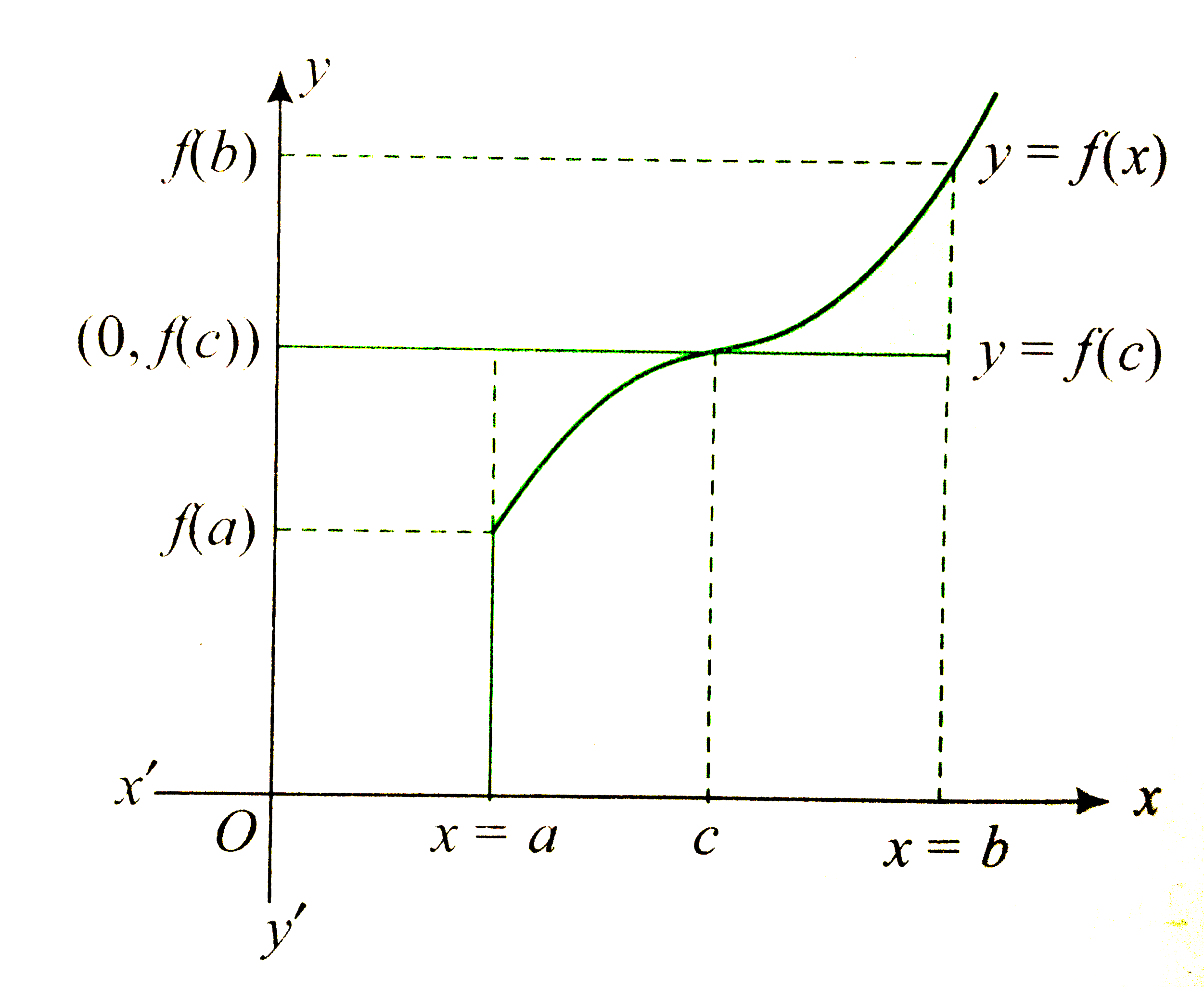
Differentiating w.r.t. c, we get
$\frac{d A}{d c} = [2 c - (a + b)] f' (c) + 2 f (c) + 0 - f (c) - (f (c) - 0)$
For maxima and minima , $\frac{d A}{d c} = 0$
$\Rightarrow f' (c) [2 c - (a + b)] = 0 (a s f' (c) \neq 0)$
Hence, $c = \frac{a + b}{2}$
$Also for c < \frac{a + b}{2}, \frac{d A}{d c} < 0 and for c > \frac{a + b}{2}, \frac{d A}{d c} > 0$
Hence, A is minimum when $c = \frac{a + b}{2}$ .
If the area enclosed by $f (x) = sin x + cos x, y = a$ between two consecutive points of extremum is minimum, then the value of a is
A0
B-1
C1
D2

CENGAGE-AREA-Comprehension Type

Home
Ask Doubt
Profile

If the area bounded by f(x)=√tanx,y=f(c),x=0andx=a,0<c<a<π2 is minimum then find the value of c.

Topper's Solved these Questions

Similar Questions

Knowledge Check

CENGAGE-AREA-Comprehension Type

If the area bounded by $f (x) = \sqrt{tan x}, y = f (c), x = 0 and x = a, 0 < c < a < \frac{π}{2}$ is minimum then find the value of c.