Find the area bounded by y2≤4x,x2+y2≥2x,andx≤y+2 in the first quadrant.Solution in Tamil
For y2≤4x, points lie on or inside parabola y2=4x for x2+y2≥2x, points lie on or outside circle (x−1)2+(y−0)2=1 For x≤y+2, points lie on or to the left side (towards origin) of the line x=y+2.
The graphs of the curves is as shown in the figure.
Solving parabola and line y=x+2, we get
(x−2)2=4x
or x2−8x+4=0
or x=8±√482=2(2±√3)=(1±√3)2
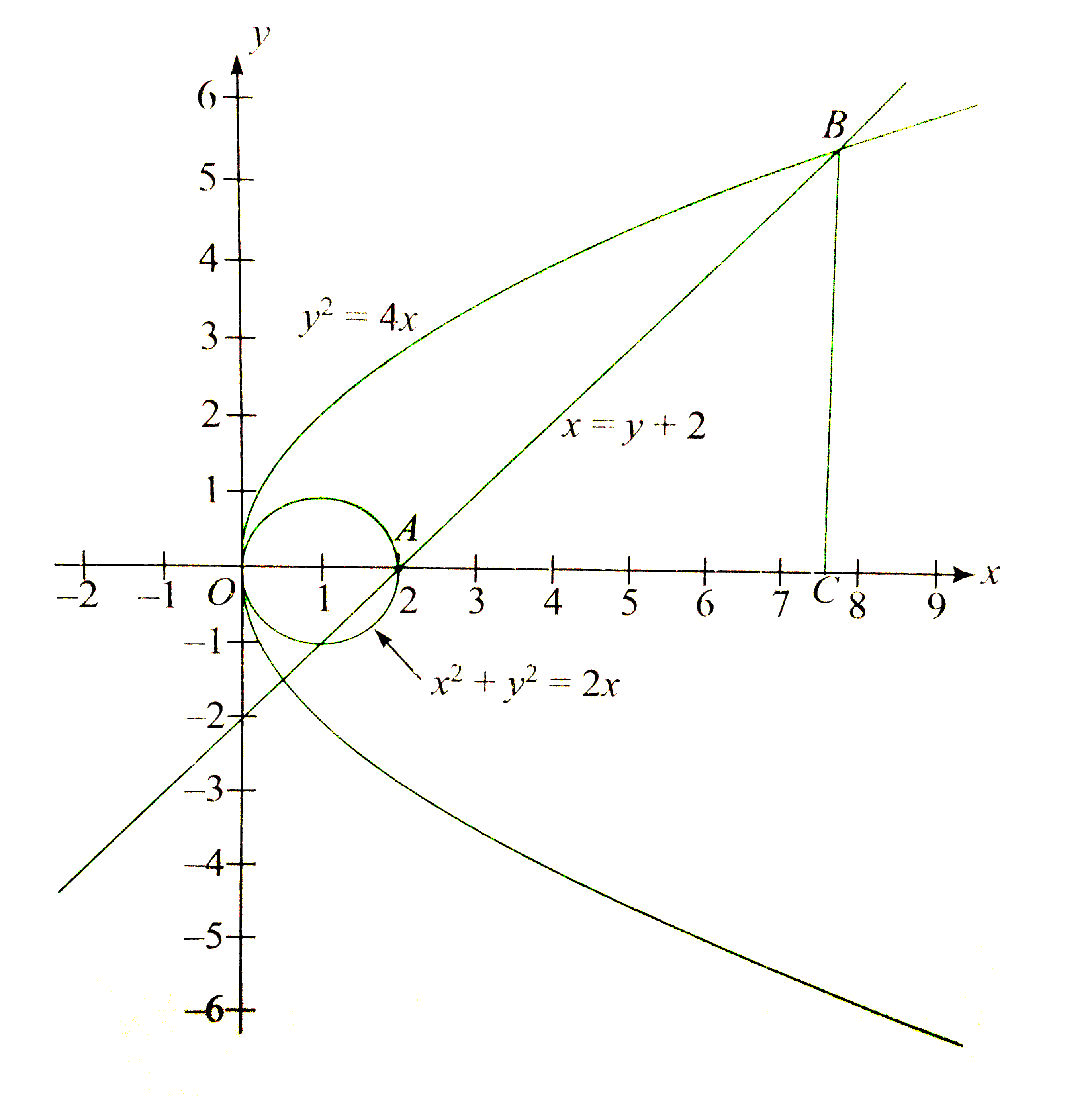
From the figure, required area is
A=(√3+1)2∫0√4xdx−Area of semicircle
=√4[2x3/23](√3+1)20−π2−12((√3+1)2−2)2(√3+1)
=4(√3+1)33−π2−2(√3+1)2
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionFind the area of the region lying in the first quadrant and bounded by y=4x2,x=0,y=1andy=4.
View SolutionFind the area bounded by the curve y=4x^(2),x=0,x=1 and y=4 in first quadrant.
View SolutionFind the area of the region if the first quadrant bounded by the parabola y2=4x, the line x+y=3 and y-axis.
View SolutionFind the area of the region lying in the first quadrant and bounded by y=4x2, x = 0, y = 1 and y = 4.
View SolutionFind the area of the region lying in the first quadrant and bounded by y=4x2, x = 0, y = 1 and y = 4.
View SolutionFind the area of the region lying in the first quadrant and bounded by y = 4x^(2), x = 0, y = 1 and y = 4.
View SolutionFind the area bounded by y2≤4x,x2+y2≥2x,andx≤y+2 in the first quadrant.
View SolutionFind the area of the region lying in the first quadrant and bounded by y=4x2,x=0,y=1andy=4.
View SolutionFind the area of the region lying in the first quadrant and bounded by y = 4x^(2), x = 0, y = 1 and y = 4.
View SolutionFind the area of the region lying in the first quadrant and bounded by y = 4x^(2), x = 0, y = 1 and y = 4.
View SolutionFind the area of the region lying in the first quadrant and bounded by y=4x2,x=0,y=1 and y=4.
View Solution