Find the area of the region lying in the first quadrant and bounded by
y=4x2,x=0,y=1 and y=4.Solution in Malayalam
The required area =5∫1xdy
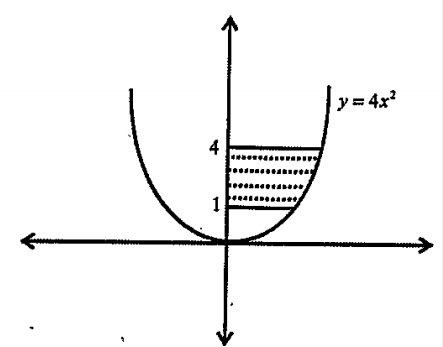
=4∫1√y2dy(y=4x2⇒x2=y4⇒x=√y2)
12[y3/23/2]41=13[43/2−13/2]
=13[23−1]=73sq.units
Topper's Solved these Questions
Similar Questions
Find the rate of change of the area of a circle with respect to its radius r when r = 5 cm.
View SolutionCheck the continuity of the function f(x)=2x+3 at x=1
View SolutionFind the area of the region bounded by x2=16y, y=1, y=4 and the y-axis in the first quadrant.
View SolutionFind the area bounded by the curve y=4x^(2),x=0,x=1 and y=4 in first quadrant.
View SolutionFind the area of the region bounded by y2=4x,x=1,x=4 and the x-axis in the first quadrant.
View SolutionSketch the region lying in the first quadrant and bounded by y=4x2 ,x = 0, y = 2 and y = 4. Find the area of the region using integration.
View SolutionFind the area of the region lying in the first quadrant bounded by the curve y2=4x, X axis and the lines x=1,x=4.
View Solutionप्रथम चतुर्थेाश में सम्मिलित एव y=4x2,x=0 y =1 तथा y = 4 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View SolutionFind the area of the region bounded by the curve y2=4x and the lines x = 1 and x = 4 lying in the first quadrant.
View SolutionFind the area of the region bounded by x2=16y,y=1,y=4 and the y-axis lying in the first quadrant using integration.
View SolutionFind the area of the region bounded by x2=16y, y=1, y=4 and the y-axis in the first quadrant.
View SolutionArea of the region bounded by x=y4,y=1andy=5 and the Y axis lying in the first quadrant is _____
View SolutionThe area of the region lying in the first quadrant and bounded by the curve y=4x2, and the lines y =2 and y =4 is "___________"
View SolutionFind area of the region bounded by 2x+4y=10,y=2andy=4 and the Y- axis lying in the first quadrant.
View SolutionFind the area of the region bounded by y2=4x,x=1,x=4 and the x-axis in the first quadrant.
View SolutionSketch the region lying in the first quadrant and bounded by y=9x2,x=0,y=1andy=4. Find the area of region using integration.
View Solution
