Find the area of the region lying in the first quadrant bounded by the curve $y^{2} = 4 x$ , X axis and the lines $x = 1, x = 4$ .

Video Solution

Text Solution

Verified by Experts

Area of the shaded region $= 4 \int 1 y . d x$

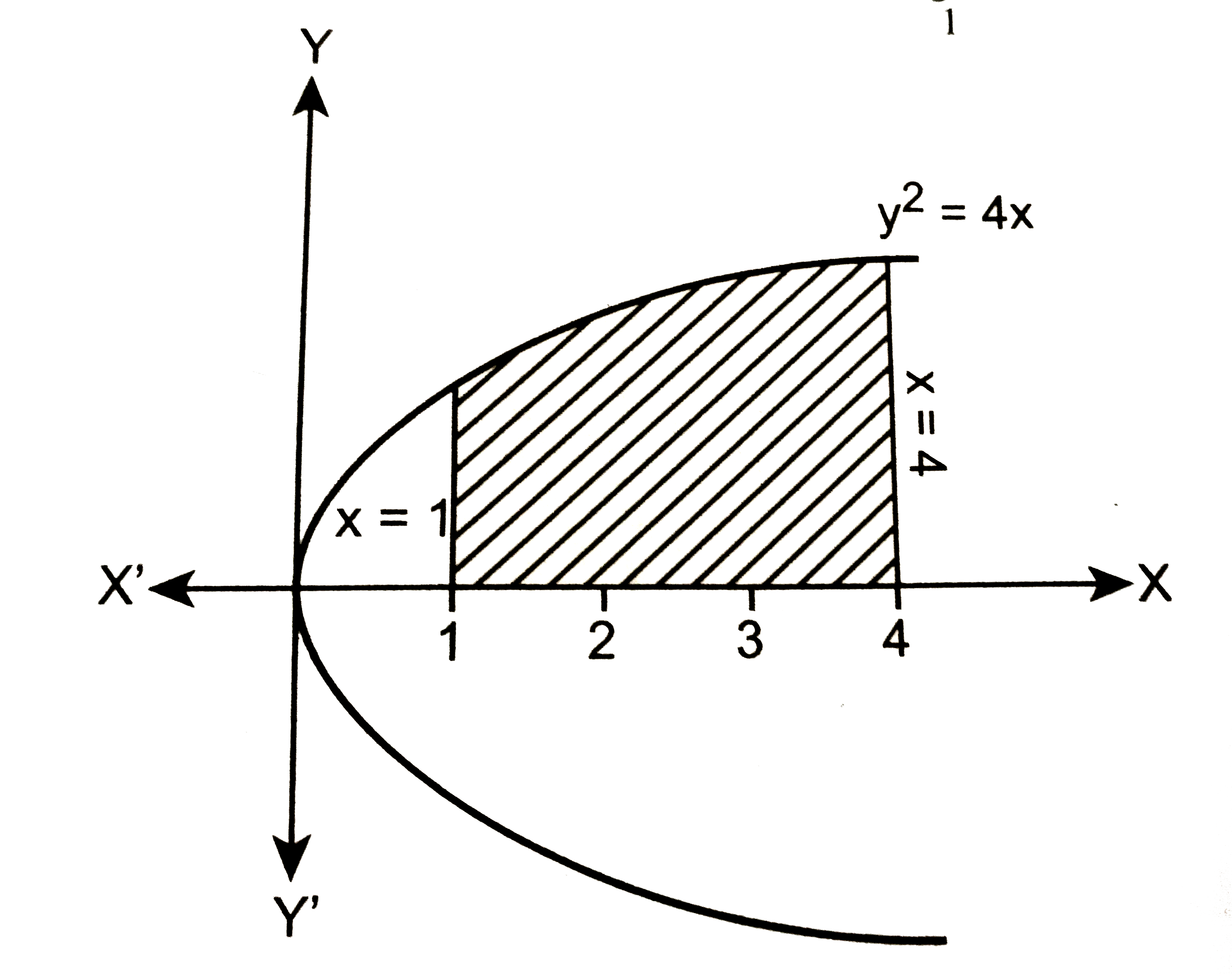
$= 4 \int 1 2 \sqrt{x} . d x (. ∵ y^{2} = 4 x given)$
$= 2 \cdot \frac{2}{3} {[x^{3 / 2}]}_{1}^{3 / 2}$
$= \frac{28}{3}$ sq. units.

Updated on:21/07/2023

Find the area lying in the first quadrant and bounded by the curve $y = x^{3}$ and the line $y = 4 x .$
A2
B3
C4
D5
Area lying in the first quadrant and bounded by the circle $x^{2} + y^{2} = 4$ and the lines $x = 0 and x = 2$ is :
A $π$
B $\frac{π}{2}$
C $\frac{π}{2}$
D $\frac{π}{4}$
Area lying in the first quadrant and bounded by the circle $x^{2} + y^{2} = 4$ and the lines $x = 0 and x = 2$ is
A $π$
B $\frac{π}{2}$
C $\frac{π}{3}$
D $\frac{π}{4} .$