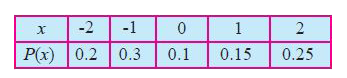
The p.m.f. for X = number of major defects in a randomly selected appliance of a certain type is
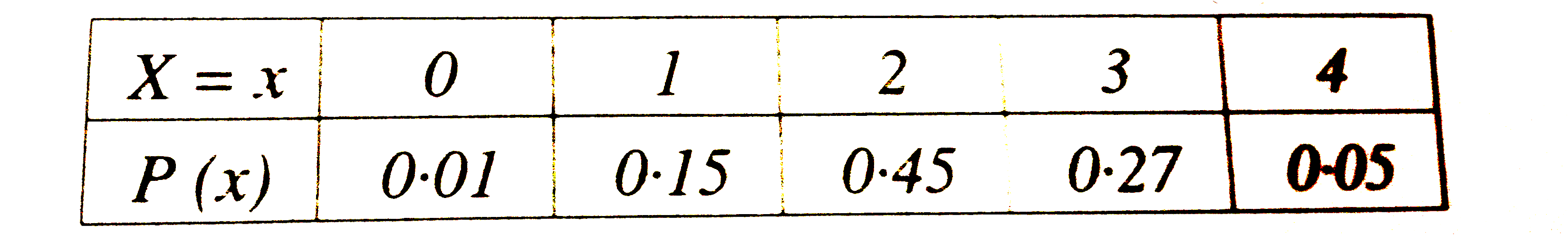
Find the expected value and variance of X.

From the table, Σxi⋅P(xi)=2.06
Σx2i⋅P(xi)=5.18
∴ Expected value of X=Σxi⋅P(xi)=2.06
Variance =V(X)=Σx2i⋅P(xi)−[Σxi⋅P(xi)]2
=5.18−(2.06)2
=5.18−4.2436=0.9364.
Topper's Solved these Questions
- JULY 2016Book:GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSChapter: JULY 2016Exercise:Section-II
Explore 20 Videos
- FEBRUARY 2020Book:GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSChapter: FEBRUARY 2020Exercise:All Questions
Explore 44 Videos
- JULY 2017Book:GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSChapter: JULY 2017Exercise:SECTION - II
Explore 20 Videos
Similar Questions
Knowledge Check
The variance of the number 2,3,11 and x is 494. Find the value of x.
A6,143B6,145C6,163DNone of these
In the p.m.f. of r.v. X

Find a
View SolutionFind the expected value and variance of r.v. X whose p.m.f. is given below.
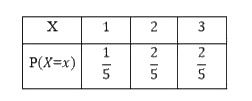
View SolutionThere are 3 defective bulbs, in a group of 10 bulbs. If X is the number of defective bulbs in a random draw of 3 bulbs, then find its mean and variance.
View SolutionA box contains 16 bulbs, out of which 4 bulbs are defective. Three bulbs are drawn at random from the box. Let X be the number of defective bulbs drawn. Find the mean and variance of X.
View SolutionThree defective bulbs are mixd with 7 good ones. Let X be the number of defective bulbs when 3 bulbs are drawn at random. Find the mean and variance of X.
View SolutionAn urn contains 5 red 2 black balls. Two balls are randomly drawn, without replacement. Let X represent the number of black balls drawn. What are the possible values of X? Is X a random variable ? if yes, find the mean and variance of X.
View SolutionA packet of 10 electronic components is known to include 3 defectives. If 4 components are selected from the packet at random, what is the expected value of the number of defective?
View Solution