From a point, P perpendicular PM and PN are drawn to x and y axes, respectively. If MN passes through fixed point (a,b), then locus of P is Solution in Tamil
The correct Answer is:C
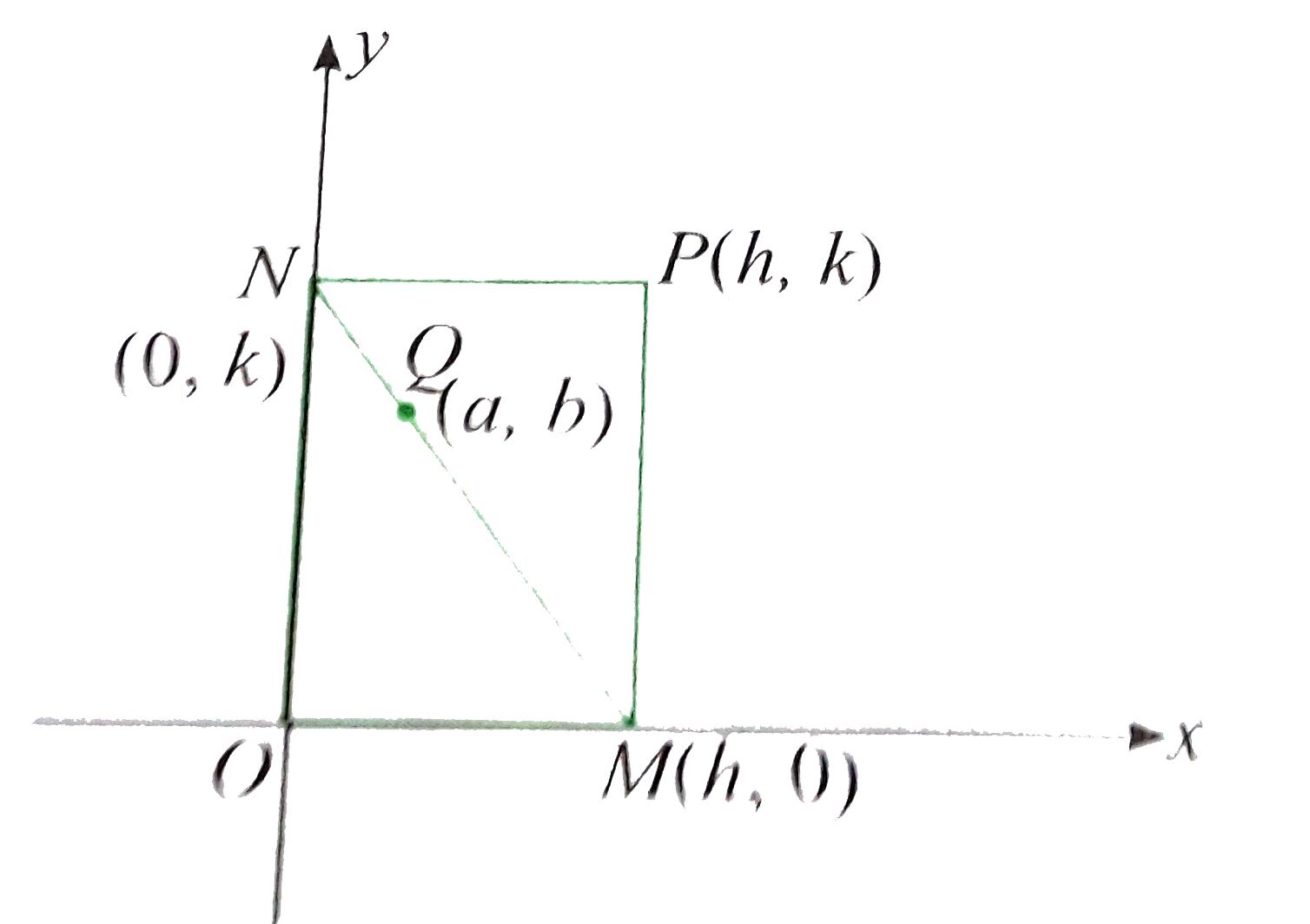
Let P(h,k)
So, points M and N are (h,0) and (0,k), respectively. passes through the point
So, M,N and Q are collinear.
Slope of MN=Slope of QM
So locus is .
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Multiple)
13 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Comprehension)
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.6
9 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
If (−6,−4),(3,5),(−2,1) are the vertices of a parallelogram, then the remaining vertex can be (0,−1) (b) 7,9) (−1,0) (d) (−11,−8)
View SolutionStudy the diagram. The line l is perpendicular to line m Does PE bisect CG?
View SolutionFind the locus of a point whose distance from (a, 0) is equal to its distance from the y-axis.
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionThe locus of the foot of the perpendicular drawn from origin to a variable line passing through fixed point (2,3) is a circle whose diameter is
View SolutionA straight line passes through a fixed point (2, 3). Locus of the foot of the perpendicular on it drawn from the origin is
View SolutionFrom a point, P perpendicular PM and PN are drawn to x and y axes, respectively. If MN passes through fixed point (a,b), then locus of P is
View SolutionFrom a point P, perpendiculars PL and PM are drawn upon X and Y axes respectively. If LM passes through a fixed point (x1,y1) then the locus of P is
View SolutionA point P is taken on the circle x2+y2=a2 and PN, PM are draw, perpendicular to the axes. The locus of the pole of the line MN is
View SolutionFind the locus of the foot of the perpendicular drawn from the origin to the straight line which passes through the fixed point (a,b).
View SolutionA variable point P is on the circle x2+y2=1 on XY-plane. From point P perpendicular PN is drawn to the line L:x-2=y-2=-z, then minimum length PN drawn is
View SolutionA straight line passes through a fixed point (6,8) : Find the locus of the foot of the perpendicular drawn to it from the origin O.
View SolutionThe locus of the foot of the perpendicular drawn from orign to a variable line passing through fixed point (2,3) is a circle whose diameter is
View SolutionFrom a point, P perpendicular PM and PN are drawn to x and y axes, respectively. If MN passes through fixed point (a,b), then locus of P is
View Solution
