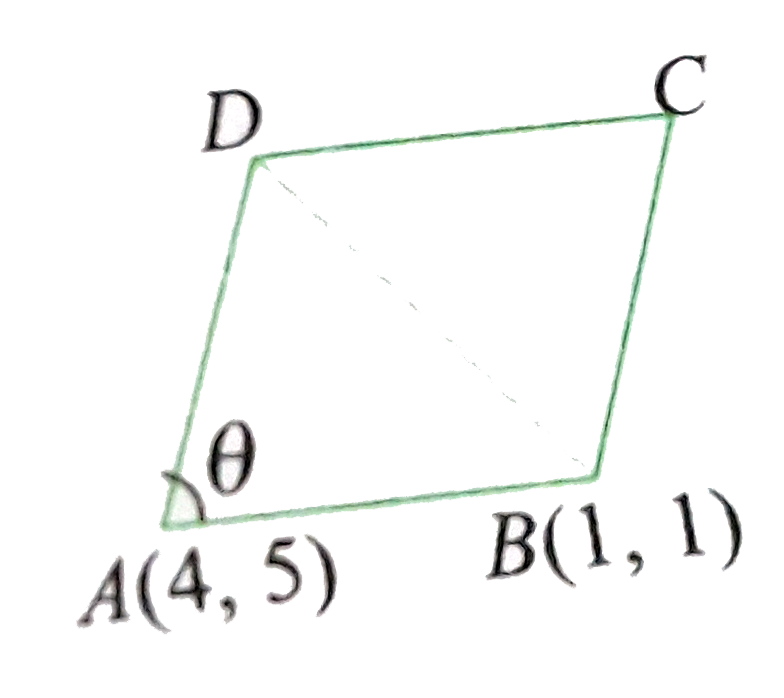
If one side of a rhombus has endpoints (4, 5) and (1, 1), then the maximum area of the rhombus is 50 sq. units (b) 25 sq. units 30 sq. units (d) 20 sq. unitsSolution in Tamil
50 sq.units
25 sq.units
30 sq.units
20 sq.units
The correct Answer is:B
From the figure Area of a rhombus =2×(Area ofΔABD)
=2×12×5×5sinθ
=25sinθ
Hence,the maximum area is 25 (when sinθ=1).
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Multiple)13videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Comprehension)10videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.69videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
If (−6,−4),(3,5),(−2,1) are the vertices of a parallelogram, then the remaining vertex can be (0,−1) (b) 7,9) (−1,0) (d) (−11,−8)
01:38View SolutionStudy the diagram. The line l is perpendicular to line m Does PE bisect CG?
05:40View SolutionFind the locus of a point whose distance from (a, 0) is equal to its distance from the y-axis.
03:49View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
02:49View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
04:15View SolutionIf one side of a rhombus has endpoints (4, 5) and (1, 1), then the maximum area of the rhombus is 50 sq. units (b) 25 sq. units 30 sq. units (d) 20 sq. units
01:41View SolutionOne diagonal of a square is 3x-4y+8=0 and one vertex is (-1, 1). The area of square is (a) 1/50 sq. unit (b) 1/25 sq. unit (c) 3/50 sq. unit (d) 2/25 sq. unit
05:40View SolutionThe area of the triangle formed by the points P(0,1),Q(0,5)andR(3,4) is (a) 16 sq. units (b) 8 sq. units (c) 4 sq. units (d) 6 sq. units
04:31View SolutionThe area bounded by the curve y=4x−x2 and x-axis is (A) 307 sq. units (B) 317 sq. units (C) 323 sq. units (D) 343 sq. units
02:18View SolutionThe area of the region bounded by the curves y=|x−1| and y=3−|x| is (A) 6 sq. units (B) 2 sq. units (C) 3 sq. units (D) 4 sq. units
03:25View SolutionIf d1 and d2 be the diagonals of a rhombus, then its area is (.....) sq units.
06:11View SolutionThe area bounded by the curves y=logex and y=(logex)2 is (A) e−2 sq. units (B) 3−e sq. units (C) e sq. units (D) e−1 sq. units
02:10View SolutionThe area bounded by the curves y=|x|−1andy=−|x|+1 is 1 sq. units (b) 2 sq. units 2√2 sq. units (d) 4 sq. units
01:57View SolutionIf one side of a rhombus has endpoints (4, 5) and (1, 1), then the maximum area of the rhombus is 50 sq. units (b) 25 sq. units 30 sq. units (d) 20 sq. units
04:16View SolutionThe area enclosed by 2|x|+3|y|≤6 is (a)3 sq. units (b) 4 sq. units (c)12 sq. units (d) 24 sq. units
07:00View SolutionIf one side of a rhombus has endpoints (4, 5) and (1, 1), then the maximum area of the rhombus is 50 sq. units (b) 25 sq. units 30 sq. units (d) 20 sq. units
01:24View Solution
