Prove that $[lim x \to 0 \frac{sin x}{x}] = 0,$ where $[.]$ represents the greatest integer function.Solution in Tamil

Video Solution

Text Solution

Verified by Experts

See the graphs of y=x and $y = {sin}^{- 1}$ x in the following figure.

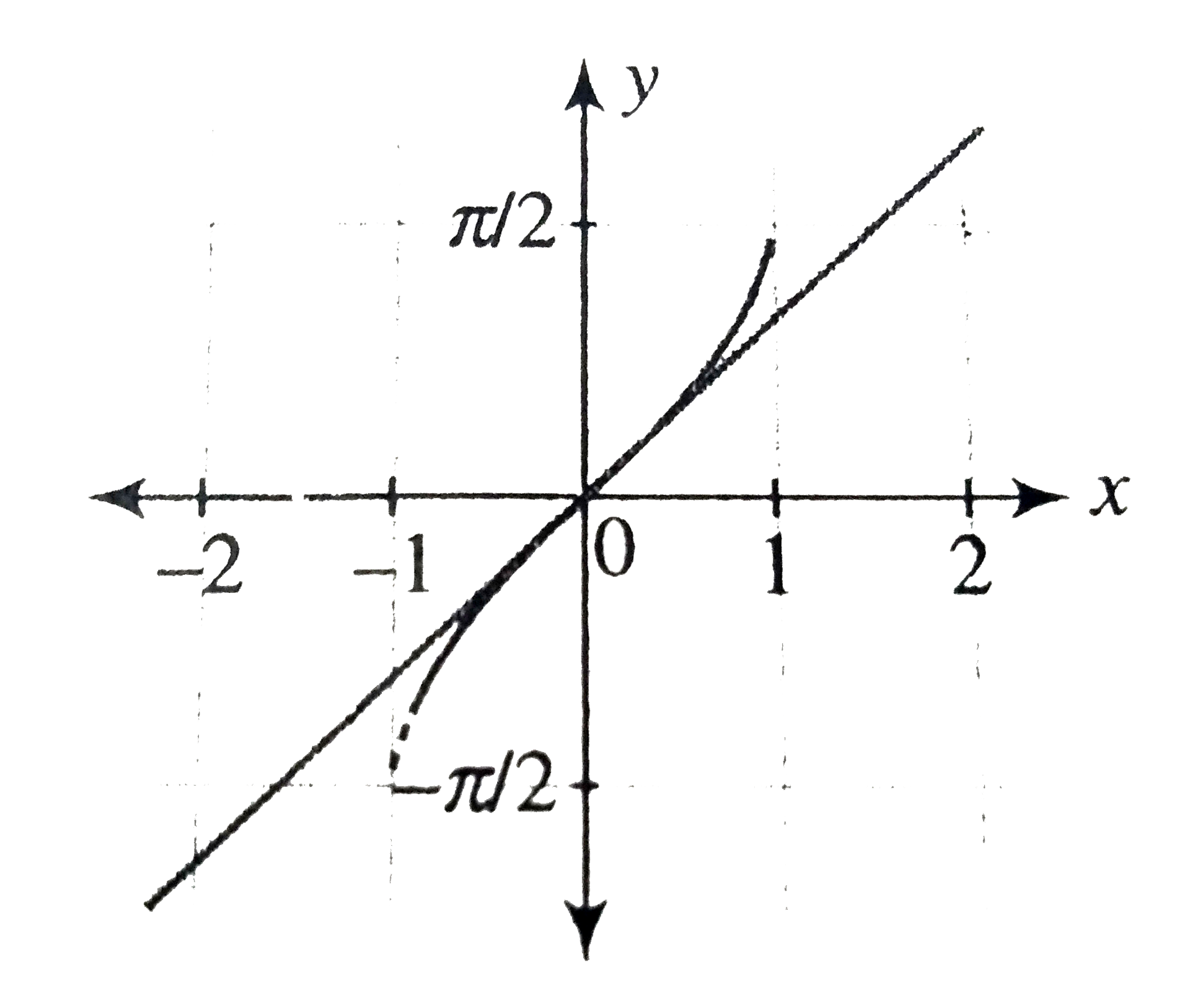
For $f (x) = {sin}^{- 1} x ∴ f' (x) = \frac{1}{\sqrt{1 - x^{2}}}$
f'(0)=1
So the curvetouches the line y=x at x=0.
For $0 < x < 1, f' (x) > 1$
So the graph of y ${sin}^{- 1} x$ lies above the graph of y=x.
From the graph, when $x \to 0^{+}$ , the graph of $y = {sin}^{- 1}$ is above the graph of y=x
or ${sin}^{- 1} x > x \Rightarrow \frac{{sin}^{- 1} x}{x} > 1 \Rightarrow [lim x \to 0^{+} \frac{{sin}^{- 1} x}{x}] = 1$
When $x \to 0^{-}$ , the graph of $y = {sin}^{- 1} x$ is below the graph of y = x
or ${sin}^{- 1} x < x \Rightarrow \frac{{sin}^{- 1} x}{x} > 1 (as x is negative) \Rightarrow [lim x \to 0^{+} \frac{{sin}^{- 1} x}{x}] = 1$
Thus, $[lim x \to 0^{+} \frac{{sin}^{- 1} x}{x}] = 1$

Updated on:21/07/2023

|

Class 12 MATHS INVERSE TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

CENGAGE-GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS-Exercise

Home
Ask Doubt
Profile