If f(x) = 0 has n roots, then f'(x) = 0 has ………..roots Solution in Tamil
Given equation is cos−1(cosx)=n−xn,x≥0
or cos−1(cosx)=1−xn,x≥0
For seven roots of equatio, the graphs of y=cos−1(coss) and y=1−xn intersect seven times.
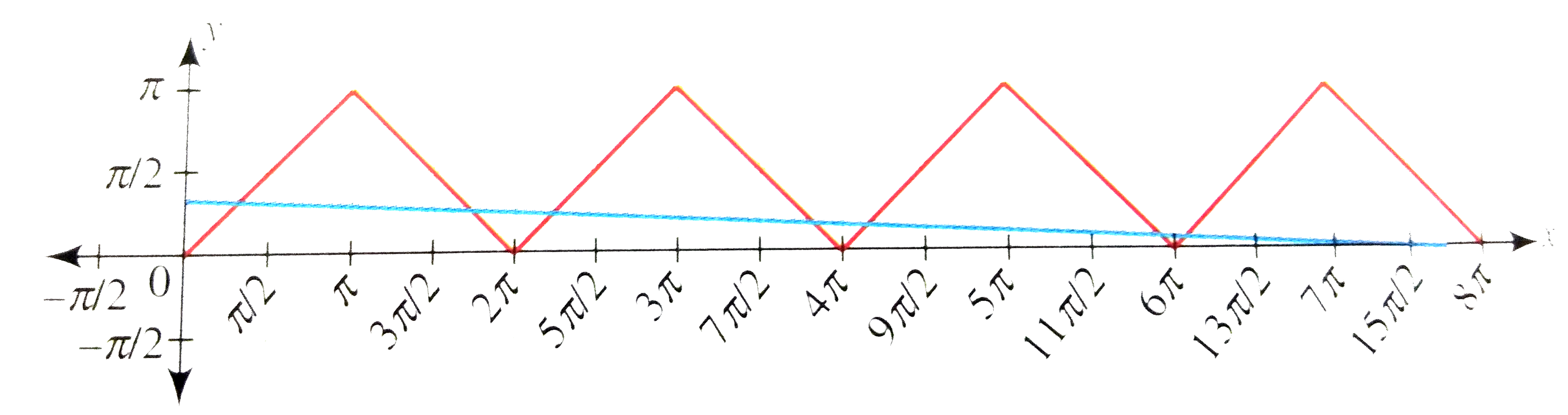
For seven roots, the line y=1−xn must meet the x-intercept is between 6π and 8π.
∴n∈(6π,8π)
Topper's Solved these Questions
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise
18 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
14 Videos
Similar Questions
Draw the graph of y=tan−1x+cot−1x
View SolutionDoes the following graph pass the vertical or horizontal line test ?

View SolutionDraw the graph of y=tan−1x−cot−1x.
View SolutionIf f(x)=|xaaaxaaax|=0, then f′(x)=0andfx=0 has common root fx=0andf′(x)=0 has common root sum of roots of f(x)=0 is −3a none of these
View SolutionLet f(x)=x^(2)+ax+b, where a,b in R. If f(x)=0 has all its roots imaginary then the roots of f(x)+f'(x)+f(x)=0 are
View SolutionIf f(x) is a polynomial of degree 5 with real coefficientssuch that f(|x|)=0 has 8 real roots,then the number of roots of f(x)=0
View SolutionIf f(x) is a polynomial of degree 5 with real coefficients such that f(|x|)=0 has 8 real roots, then f(x)=0 has
View SolutionA polynomial of 6th degree f(x) satisfies f(x)=f(2−x),∀x∈R, if f(x)=0 has 4 distinct and 2 equal roots, then sum of the roots of f(x)=0 is
View SolutionIf f(x) = 0 has n roots, then f'(x) = 0 has ………..roots
View SolutionLet f(x)=x2+ax+b, where a, b ∈R . If f(x) =0 has all its roots imaginary , then the roots of f(x) + f'(x) + f(x) =0 are :
View SolutionIf f(x)=1+xm(x−1)n,m,n∈N, then f'(x)=0 has atleast one root in the interval
View SolutionLet f(x)=x2+ax+b, where a,b∈R. If f(x)=0 has all its roots imaginary, then the roots of f(x)+f'(x)+f''(x)=0 are
View SolutionIf f(x) be a quadratic polynomial such that f(x)=0 has a root 3 and f(2)+f(−1)=0 then other root lies in
View SolutionA polynomial of 6th degree f(x) satisfies f(x)=f(2−x),∀x∈R, if f(x)=0 has 4 distinct and 2 equal roots, then sum of the roots of f(x)=0 is
View SolutionA function f(x) is such that f(x)=0 has 8 distinct real roots and f(x)=f(6−x) for x∈R. Sum of real roots of the equation f(x)=0 is
View SolutionIf f(x)=|xaaaxaaax|=0, then f′(x)=0andfx=0 has common root fx=0andf′(x)=0 has common root sum of roots of f(x)=0 is −3a none of these
View Solution
