Find the value of $100 π \int 0 {sin}^{- 1} (sin x) d x$ .Solution in Tamil

Video Solution

Text Solution

Verified by Experts

$f (x) = {\begin{matrix} {sin}^{- 1} (sin x) + {cos}^{- 1} (cos x) & 0 \leq x < π {sin}^{- 1} (sin x) + {cos}^{- 1} (cos x) & π \leq x \leq 2 π \end{matrix}$
$⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} x + x & 0 \leq x < \frac{π}{2} (π - x) + x & \frac{π}{2} \leq x < π - (π - x) + 2 π - x & π \leq x < \frac{3 π}{2} - (x - 2 π) + 2 π - x & \frac{3 π}{2} \leq x \leq 2 π \end{matrix}$
$= ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} 2 x & 0 \leq x < \frac{π}{2} π & \frac{π}{2} \leq x < π π & π \leq x < \frac{3 π}{2} 4 π - 2 x & \frac{3 π}{2} \leq x \leq 2 π \end{matrix}$

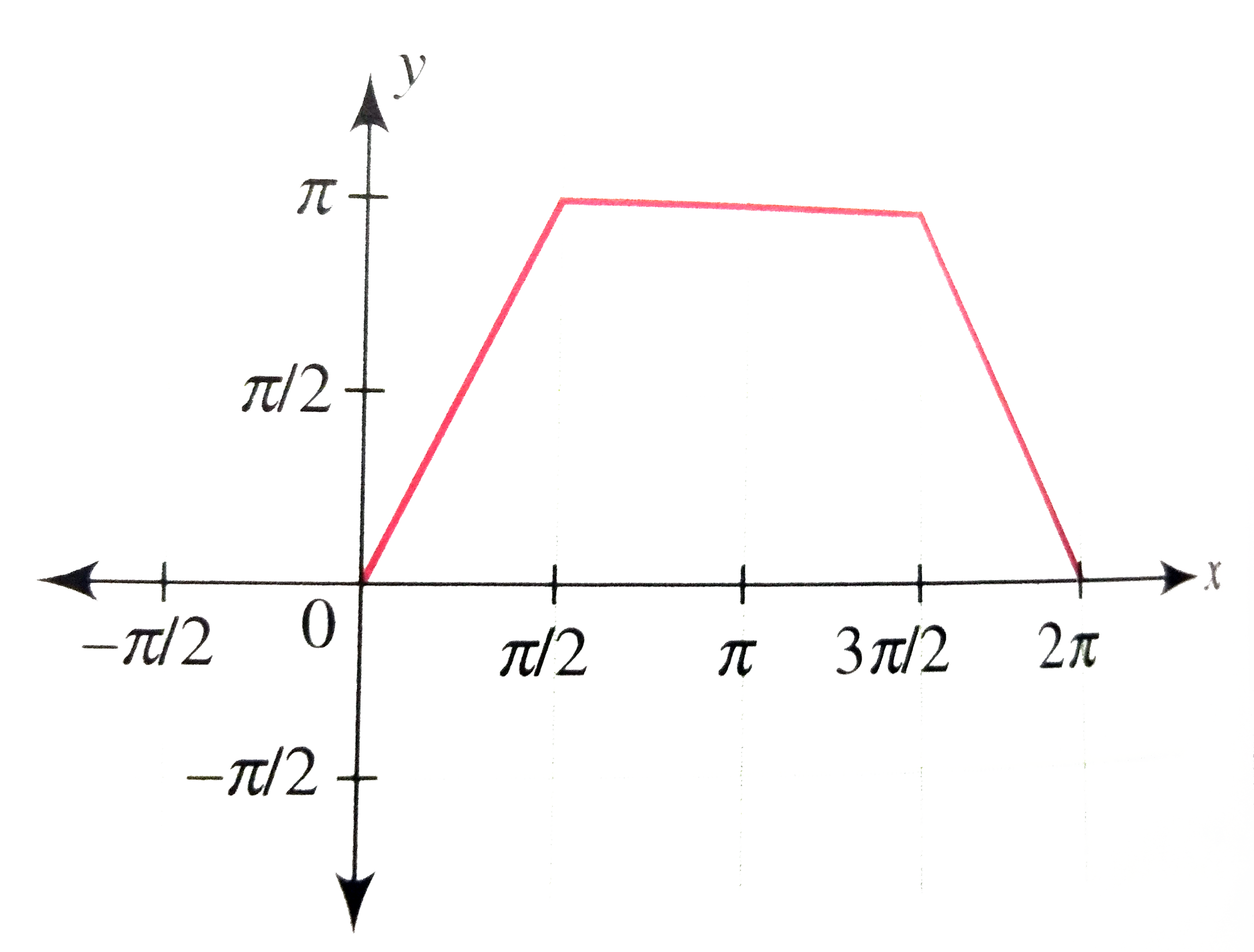
So the graph of the function for $x \in [0, 2 π]$
is as shown inthe adjacent figure.
Now f(x) is a periodic function with period $2 π$ , then the graph of $y = f (x)$ for its domain is as follows.

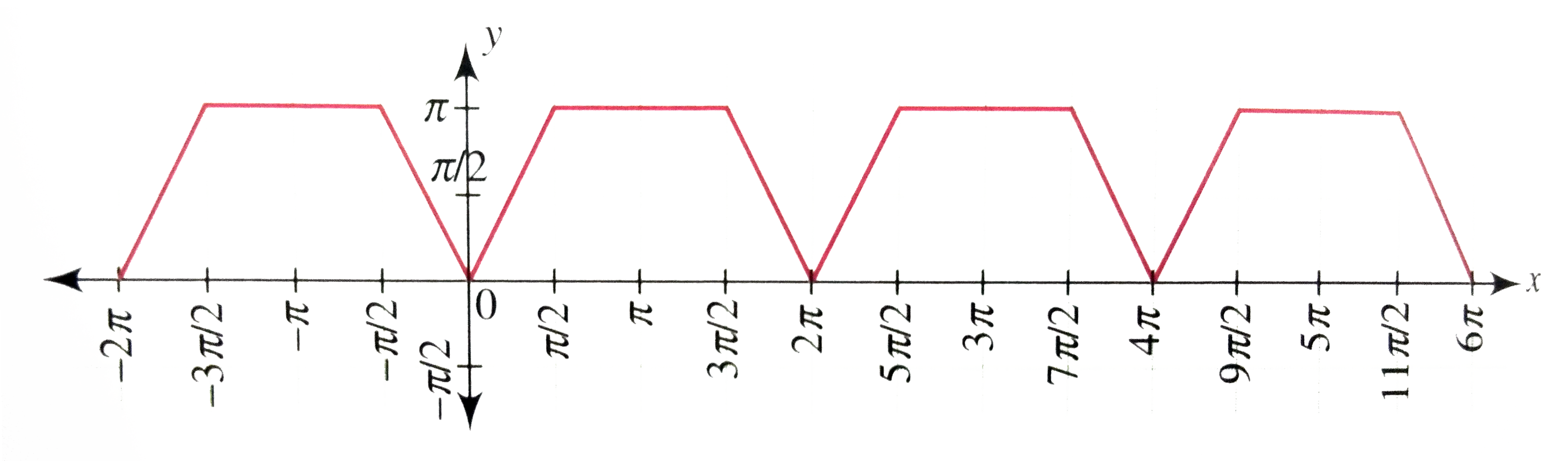
From the graph, the range of the function is $[0, π]$
Function is non-differentiable at $x = 2 n π and x = (2 n + 1) \frac{π}{2}, n \in Z$
$10 π \int 0 [{sin}^{- 1} | sin x | + {cos}^{- 1} (cos x)] d x$
$= 5 \times (Area of trapezium formed by the x-axis and the curve in [0, 2 π])$
$= 5 \times (\frac{1}{2} π (2 π + π))$
$= \frac{15 π^{2}}{2}$

Updated on:21/07/2023

|

Class 12 MATHS INVERSE TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

CENGAGE-GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS-Exercise

Home
Ask Doubt
Profile