Consider a ΔABC in which sides AB and AC are perpendicular to x-y-4=0 and 2x-y-5=0, repectively. Vertex A is (-2, 3) and the circumcenter of ΔABC is (3/2, 5/2).
The equation of the line in List I is of the form ax+by+c=0, where a,b,c∈I. Match it with the corresponding value of c in list II and then choose the correct code.

Codes :
abcdrspqsrqpqpsrrpsqSolution in Tamil
The correct Answer is:3
a.
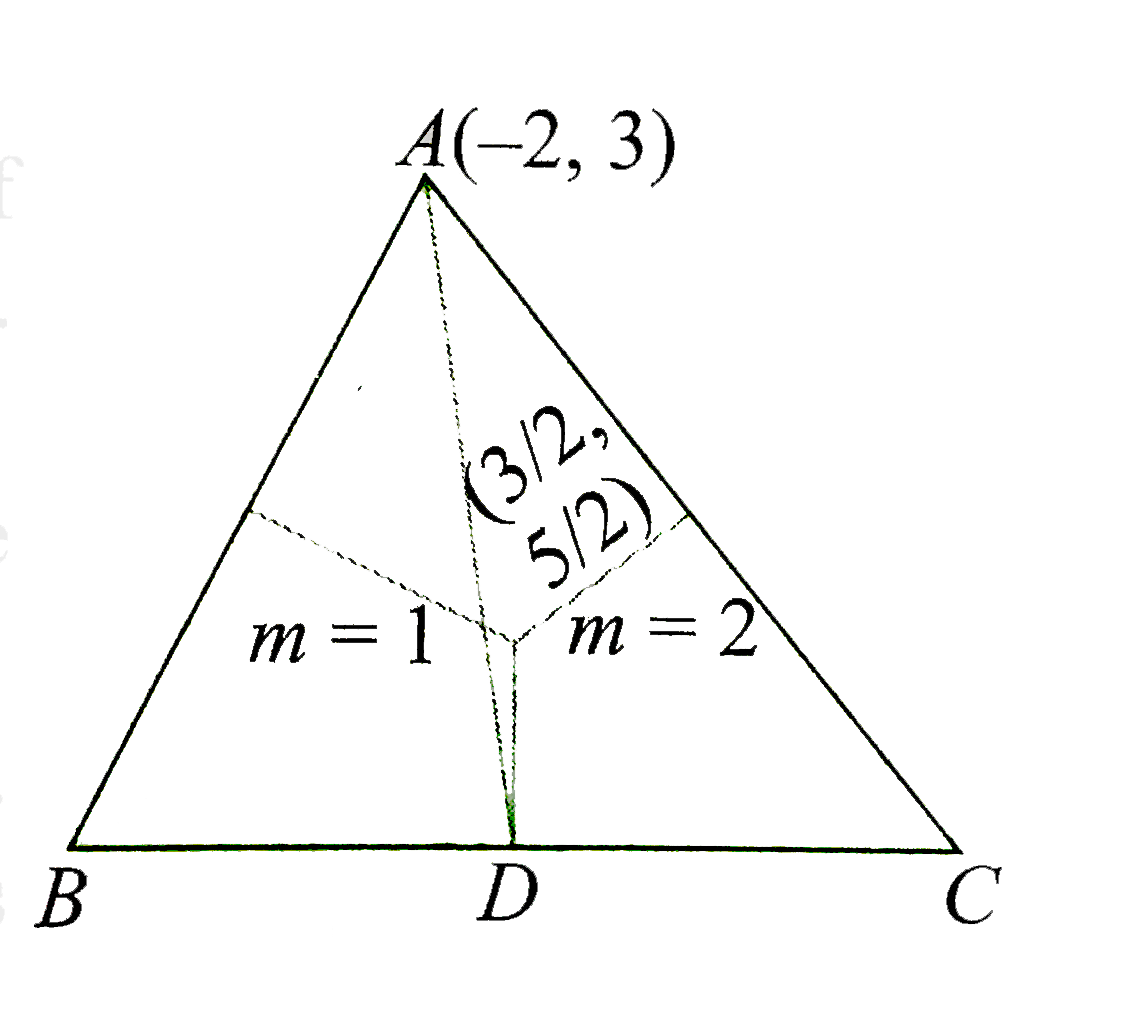
The perpendicular bisector of AB is parallel to x-y-4=0.
Therefore, the slope is 1.
It is passing through the circumcenter, i.e, (3/2, 5/2).
Therefore, the line is x-y+1 =0.
b. The perpendicular bisector of AC is B parallel to 2x-y-5=0.
Therefore, the slope is 2.
It is passing through the circumcenter, i.e., (3/2, 5/3).
Therefore, the line is 4x-2y-1=0.
c. The equation of perpendicular bisector to AC is 2x-y-5=0.
Therefore, the equation of AC can be x+2y+λ=0.
It is passing through A(-2, 3). Therefore,
λ=−4
Therefore, the equation of AC is x+2y-4=0.
d. The image of A on the perpendicular bisector of AC is
x+24=y−3−2=−2(−8−6−1)16+4=32
∴C≡(4,0)
The image of A on the perpendicular bisector of AB is
x+21=y−3−1=−2(−2−3+1)1+1=4
Therefore, B is (2, -1).
Therefore, the midpont of BC is D (3, -1/2).
Hence, the median through A is 7x+10y-16=0.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Numerical)
13 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Main Previous Year
9 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
straight line L with negative slope passes through the point (9,4) cuts the positive coordinate axes at the point P and W As L. Varies, find the minimum value of |OP|+|OQ| , where O is origin .
View SolutionThe line L given by x5+yb=1 passes through the point (13,32).the line K is parallel to L and has the equation xc+y3=1 then the distance between L and K is
View SolutionLet L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionMatch column I with column II and select the correct option from the codes given below.
View SolutionConsider a ΔABC in which sides AB and AC are perpendicular to x-y-4=0 and 2x-y-5=0, repectively. Vertex A is (-2, 3) and the circumcenter of ΔABC is (3/2, 5/2).
The equation of the line in List I is of the form ax+by+c=0, where a,b,c∈I. Match it with the corresponding value of c in list II and then choose the correct code.

Codes :
abcdrspqsrqpqpsrrpsq
View SolutionMatch the following lists:

View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionIf the sine of the angles of ΔABC satisfy the equation c3x3−c2(a+b+c)x2+lx+m=0
(where a,b,c are the sides of ΔABC), then ΔABC is
View SolutionMatch the followings (column I with column II)
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C03_E01_011_Q01.png" width="80%"gt
View SolutionMatch column I with column II
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C16_E01_002_Q01.png" width="80%"gt
View SolutionMatch column I with column II:
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C18_E01_003_Q01.png" width="80%"gt
View SolutionMatch Column I with Column II: ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C20_E01_010_Q01.png" width="80%"gt
View SolutionGiven the circle C with the equation x2+y2−2x+10y−38=0. Match the List I with the List II given below concerning C.
List IList IIA.The equation of the polar ofI.y+5=0(4, 3) with respect to CB.The equation of the tangent atII.x=1(9, -5) on CC.The equation of the normal atIII.3x+8y=27(-7, -5) on CD.The equation of the diameter ofIV.x+y=3C passing through (1, 3)V.x=9
The correct answer is
View Solution
