Given the circle C with the equation x2+y2−2x+10y−38=0. Match the List I with the List II given below concerning C.
List IList IIA.The equation of the polar ofI.y+5=0(4, 3) with respect to CB.The equation of the tangent atII.x=1(9, -5) on CC.The equation of the normal atIII.3x+8y=27(-7, -5) on CD.The equation of the diameter ofIV.x+y=3C passing through (1, 3)V.x=9
The correct answer is Solution in Telugu
ABCCIIIIVII
ABCCIVVIII
ABCCIIIVIII
ABCCIVIIIV
The correct Answer is:C
Step by step video, text & image solution for Given the circle C with the equation x^(2) + y^(2) - 2x + 10y - 38 = 0. Match the List I with the List II given below concerning C. {:(,"List I",,"List II"),(A.,"The equation of the polar of",I.,y + 5 = 0),(,"(4, 3) with respect to C",,),(B.,"The equation of the tangent at",II.,x = 1),(,"(9, -5) on C",,),(C.,"The equation of the normal at",III.,3x + 8y = 27),(,"(-7, -5) on C",,),(D.,"The equation of the diameter of",IV.,x + y = 3),(,"C passing through (1, 3)",,),(,,V.,x = 9):} The correct answer is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
x=1+31!×16+3×72!(16)2+3×7×113!(16)3+…⇒x4=
View SolutionIf α,β are the roots of the equation x2−4x+8=0. Them for any n∈N,α2n+β2n equals
View SolutionMatch list I with list II and select the correct answer: List I (Product) List II (Digit in the units place) (1827)16 1 (2153)19 (2) 3 C. (5129)21 (3) 5 (4) 7 (5) 9 A B C A B C (a) 1 4 3 (b) 4 2 3 A B C A B C (c) 1 4 5 (d) 4 2 5
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists: List I (Time) List II (Angle between hour hand and and minute hand of a clock) A. 1.10 p.m. 1. 20o B. 2.15 p.m. 2. 2212o C. 8.40 p.m. 3. 24o 4. 25o 5. 30o A B C A B C (a) 4 2 1 (b) 4 3 2 (c) 5 2 1 (d) 4 3 2
View SolutionMatch the following {:(,"List -I",,"List -II",),(A,P_(c),(i),3b,),(B,V_(c),(ii),8a//27bR,),(C,T_(c),(iii),a//27 b^(2),):}
View SolutionList-I contains angles in radians and List-II contains the quadrant in which the angle lies.
∣∣ ∣ ∣ ∣ ∣ ∣∣List-IList-II(P)2c(1)I(Q)4c(2)II(R)6c(3)III(S)7c(4)IV∣∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionIn respect of the equation [2346][xy]=[ 5c−5]
correctly match List I with List II and select the correct answer using the code given below the lists :
List IList II(Value of c))(Nature of the Equation)A.51.The equation has no solution.B.102.The equation has a unique solution.C.153.The equation has an infinite set of solution.4.The equation has two infinite sets of independent solution
View SolutionLet αandβ be the roots of the quadratic equation ax2+bx+c=0 . Observe the lists given below:
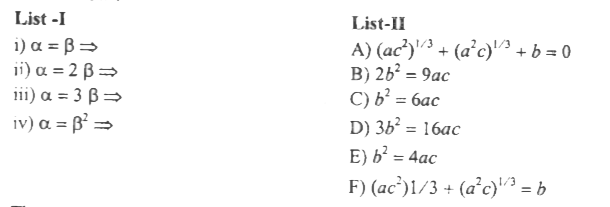
Let correct match of List -I from List -II is
View SolutionFor the circle C with the equation x2+y2−16x−12y+64=0 match the list-I with the list-II given below:
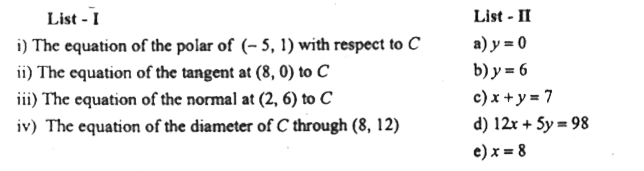
View SolutionGiven the circle C with the equation x2+y2−2x+10y−38=0 Match the List-I with the List-II given below concening C:

View SolutionFor the ellipse (x^(2))/(25)+(y^(2))/(16) = 1 , a list of lines given in List I are to be matched with their equation given in List II.
View SolutionFor the circle C with the equation x2+y2−16x−12y+64=0 match the List I with the List II given below,
List IList II(i)The equation of the polar(A)y=0of (-5, 1) with respect to C(ii)The equation of the tangent(B)y=6at (8, 0) to C(iii)The equation of the normal(C)x+y=7at (2, 6) to C(iv)The equation of the diameter(D)13x+5y=98of C through (8, 12)(E)x=8
The correct match is
View SolutionFor the ellipse x225+y216=1 a list of lines given in List I are to be matched with their equations given in Lisht II.
The correct match is:
View SolutionFor the parabola y2+6y−2x+5=0, match the items in List-I with the suitable item in List-II given below:
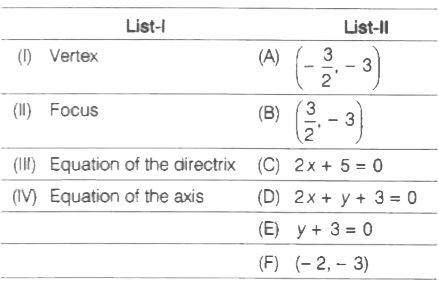
The correct matching is
View SolutionIf 1(1−2x)2(1−3x)=A1−2x+B(1−2x)2+C1−3x then match the following
List - I List - III) A(a) 9II) B(b) -6III) C(c) -2
View Solution

