A straight line with negative slope passing the point (1, 4) meets the coordinate axes at A and B. The minimum value of OA + OB = Solution in Tamil
The correct Answer is:a→s; b→p; c→q; q→r
(a)
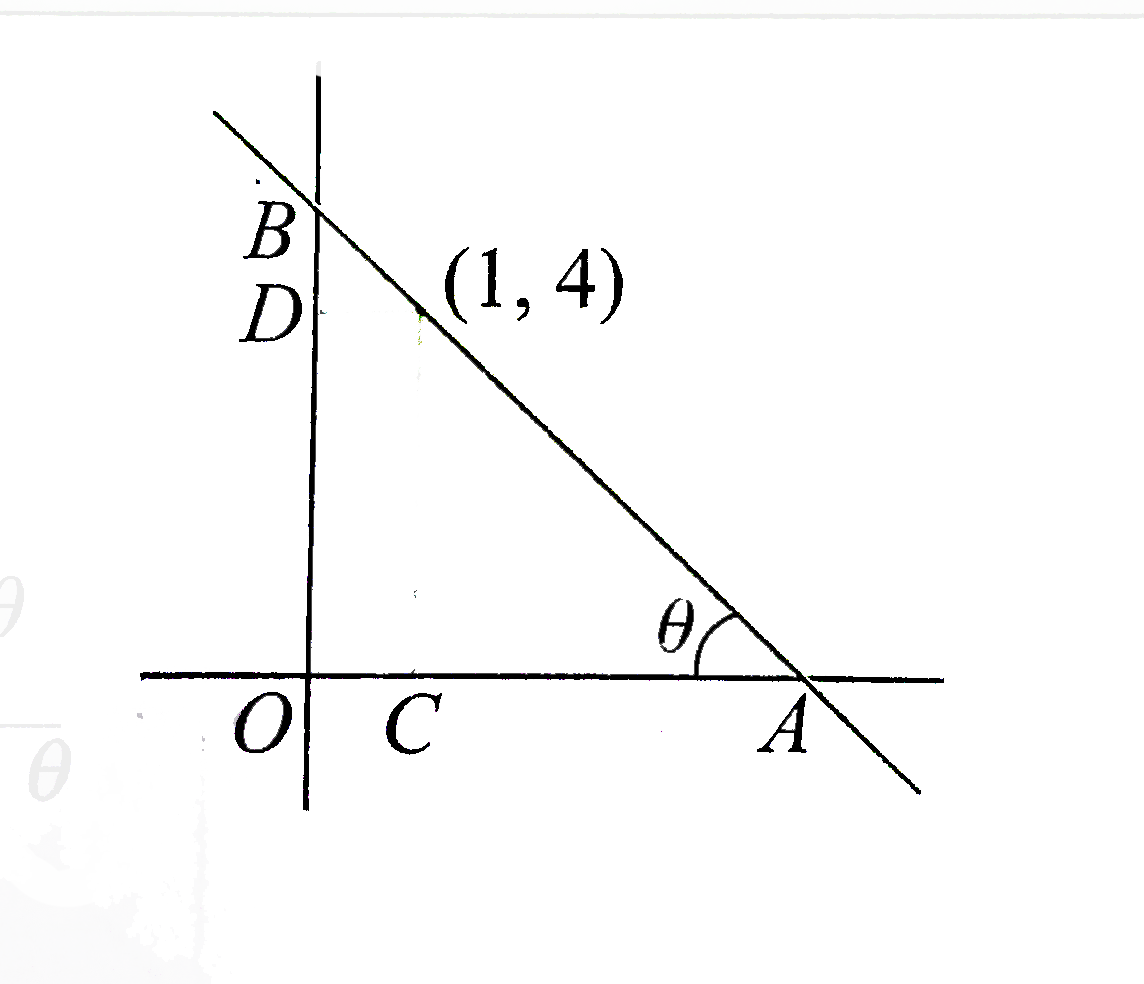
OA=1+4cotθ
OB=4+tanθ
OA+OB=5+4cotθ+tanθ
≥5+2√4cotθ tanθ
=5+(2×2)=9
(b)
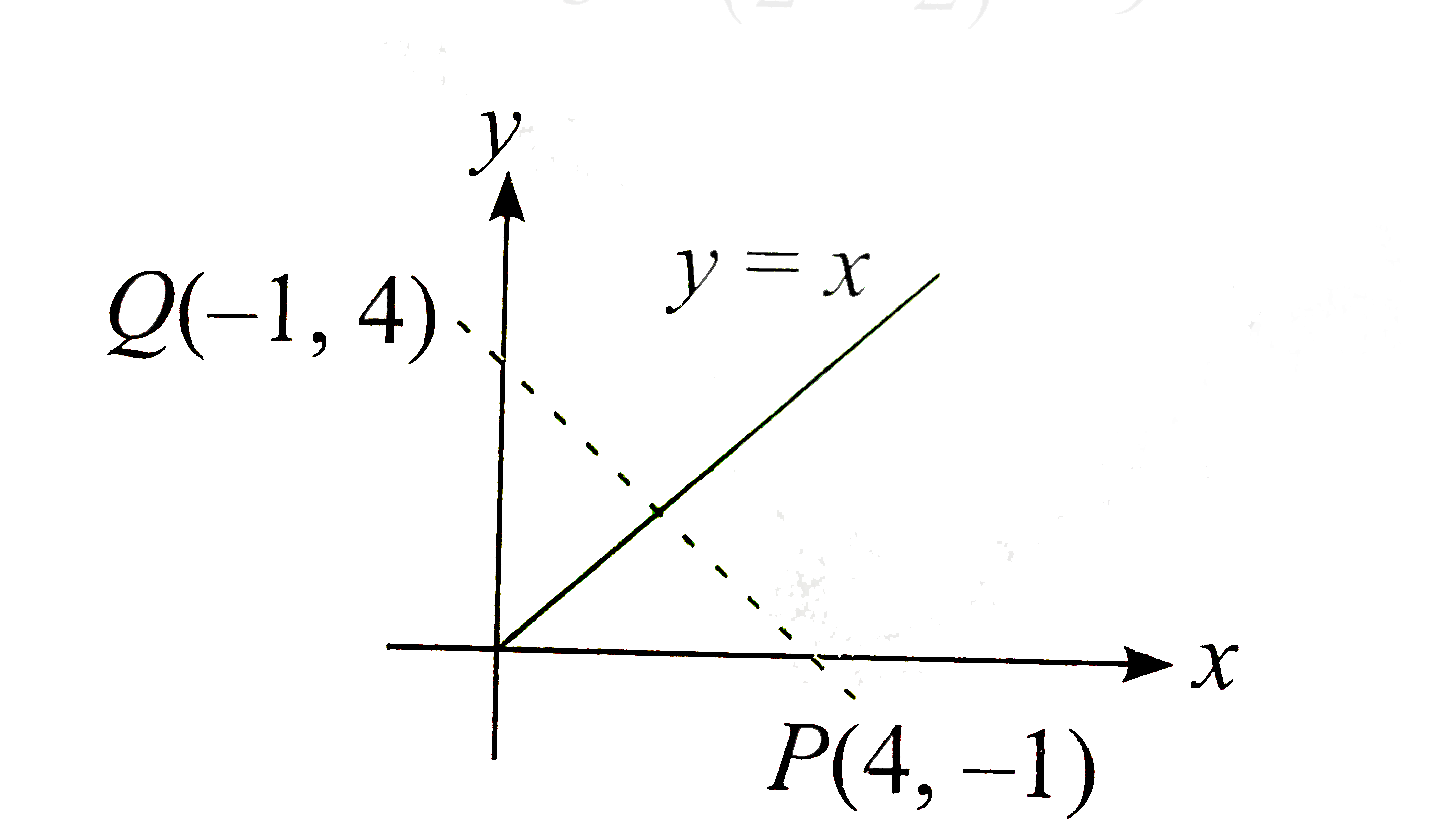
The reflection of P(4, -1) on y=x is Q (-1, 4). Hence,
PQ=√(4+1)2+(−1−4)2=√50=5√2
(c)
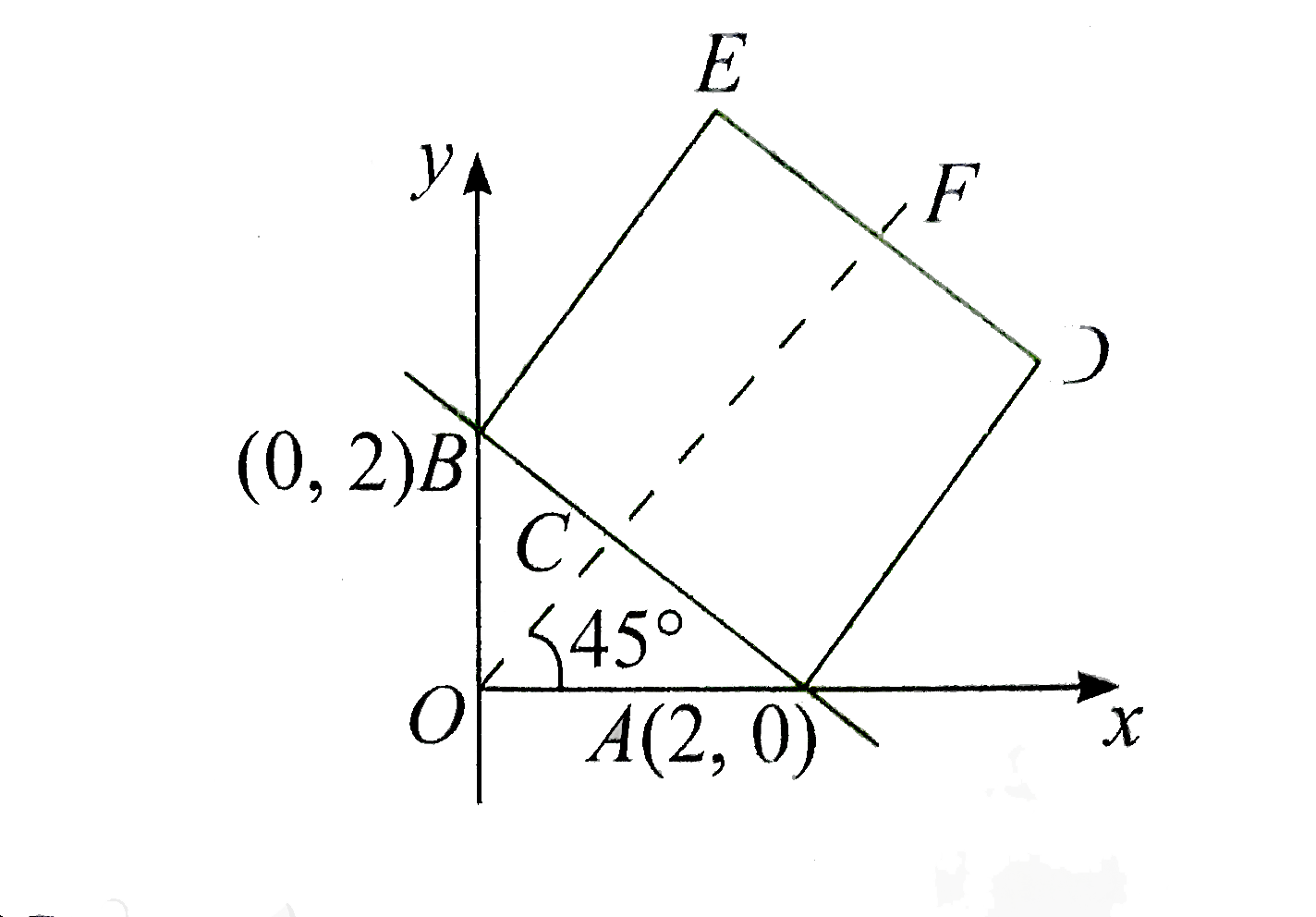
AB=2√2
OC=√2
The maximum value of d is
OF=√2+2√2
=3√2
(d) The given line is
x=4+1√2(y+1√2 or y=2x−9
Hence, the intercept made by the x-axis is 9/2.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Numerical)
13 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Main Previous Year
9 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
straight line L with negative slope passes through the point (9,4) cuts the positive coordinate axes at the point P and W As L. Varies, find the minimum value of |OP|+|OQ| , where O is origin .
View SolutionThe line L given by x5+yb=1 passes through the point (13,32).the line K is parallel to L and has the equation xc+y3=1 then the distance between L and K is
View SolutionLet L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionPoint A and B are in the first quadrant,point O is the origin. If the slope of OA is 1,slope of OB is 7 and OA=OB,Then slope of AB is: a. -1/5 b. -1/4 c. -1/3 d. -1/2
View SolutionPoint A and B are in the first quadrant; point O is the origin. If the slope of OA is 1, the slope of OB is 7, and OA=OB, then the slope of AB is −15 (b) −14 (c) −13 (d) −12
View SolutionA straight line with negative slope passing through the point (2,8) cuts the cordinate axes at A and B then minimum value of OA+OB (where 0 is origin) is equal to
View Solutionउस सरल रेखा का समीकरण निकालें जो बिंदु (-6, 6) से होकर जाती है तथा अक्षों से क्रमशः ऐसे अंतःखंड OA, OB काटती है ताकि OA -OB = 1.
View Solutionबिन्दु A के निर्देशांक (2,3,4) तथा बिन्दु B के निर्देशांक (1,-2,1) है , O मूलबिन्दु है । सिद्ध कीजिए कि OA रेखा OB पर लम्ब है ।
View SolutionA strainght line L with negative slope passes through the point (1,1) and cuts the positve coordinates axes at the points A and B . If O is the origin , thene the minimum value of OA+OBas L varies , is
View Solutionstraight line L with negative slope passes through the point (9,4) cuts the positive coordinate axes at the point P and W As L. Varies, find the minimum value of |OP|+|OQ| , where O is origin .
View SolutionA straight line with negative slope passing through the point (1,4) meets the coordinate axes at A and B.The minimum value of OA+OB is equal to
View SolutionA straight line L with negative slope passes through the point (8,2) and cuts the positive coordinate axes at the points P and Q .as L varies, the absolute minimum value of OP+OQ2O is origin is
View SolutionPoint A and B are in the first quadrant,point O is the origin. If the slope of OA is 1,slope of OB is 7 and OA=OB,Then slope of AB is: a. -1/5 b. -1/4 c. -1/3 d. -1/2
View Solution
