[Tamil] Let a function f(x) be defined in [-2, 2] as f(x) = {{:({x}"

Draw the graph of $y = \frac{1}{(1 / x)}$ .

Sketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) $f (0) = 0, f (1), lim x \to \infty f (x) = 0, f is odd$
(ii) $lim x \to 0^{+} f (x) = \infty, lim x \to 0^{-} f (x) = - \infty, lim x \to \infty f (x) = 1, lim x \to - \infty f (x) = 1$
(iii) $lim x \to - 2 f (x) = \infty, lim x \to - \infty f (x) = 3, lim x \to \infty f (x) = 3, f (0) = 0$

Let a function f(x) be defined in [−2,2] as f(x)=⎧⎪⎨⎪⎩{x},−2≤x<−1|sgn x|,−1≤x≤1{−x},1<x≤2 where {x} and sgn x denote fractional part and signum functions, respectively. Then find the area bounded by the graph of f(x) an the x-axis. Solution in Tamil

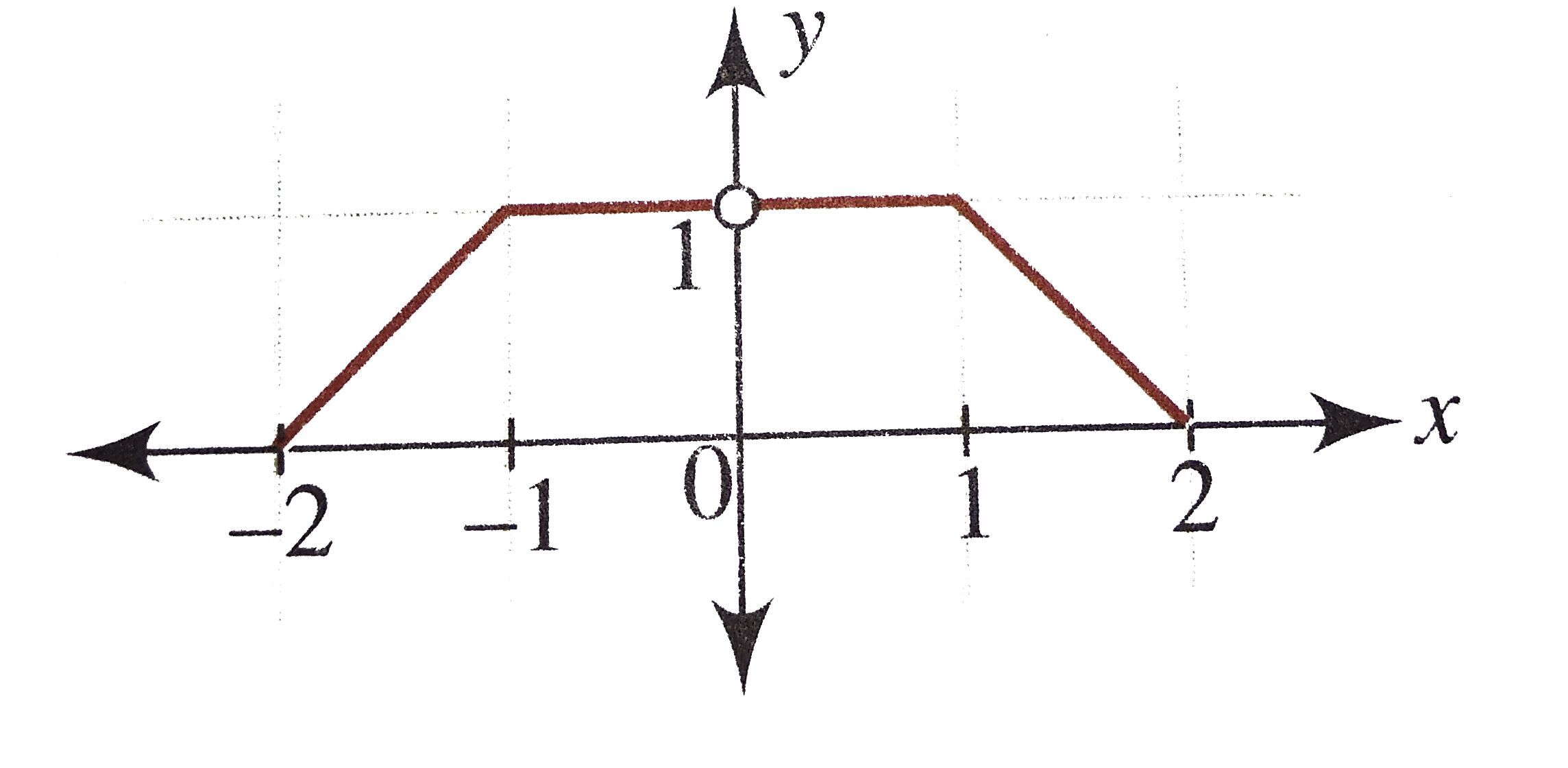
f(x)=⎧⎪⎨⎪⎩{x},−2≤x<−1|sgn x|,−1≤x≤1{−x},1<x≤2 =⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩x+2,−2≤x<−11,−1≤x<0,0,x=01,0<x≤1−x+2,1<x≤2 The graph fo the function is as shown in the following figure. Area =2+42×1=3 sq. units

Topper's Solved these Questions

Similar Questions

CENGAGE-GRAPHS OF ELEMENTARY FUNCTIONS -Exercise