Let a, b, c real. If ax2+bx+c=0 has two real roots αandβ, where α<−1andβ>1, then show that 1+ca+∣∣∣ba∣∣∣<0Solution in Tamil
Let f(x)=x2+bax+ca.
According to the questions, we have the following graph.
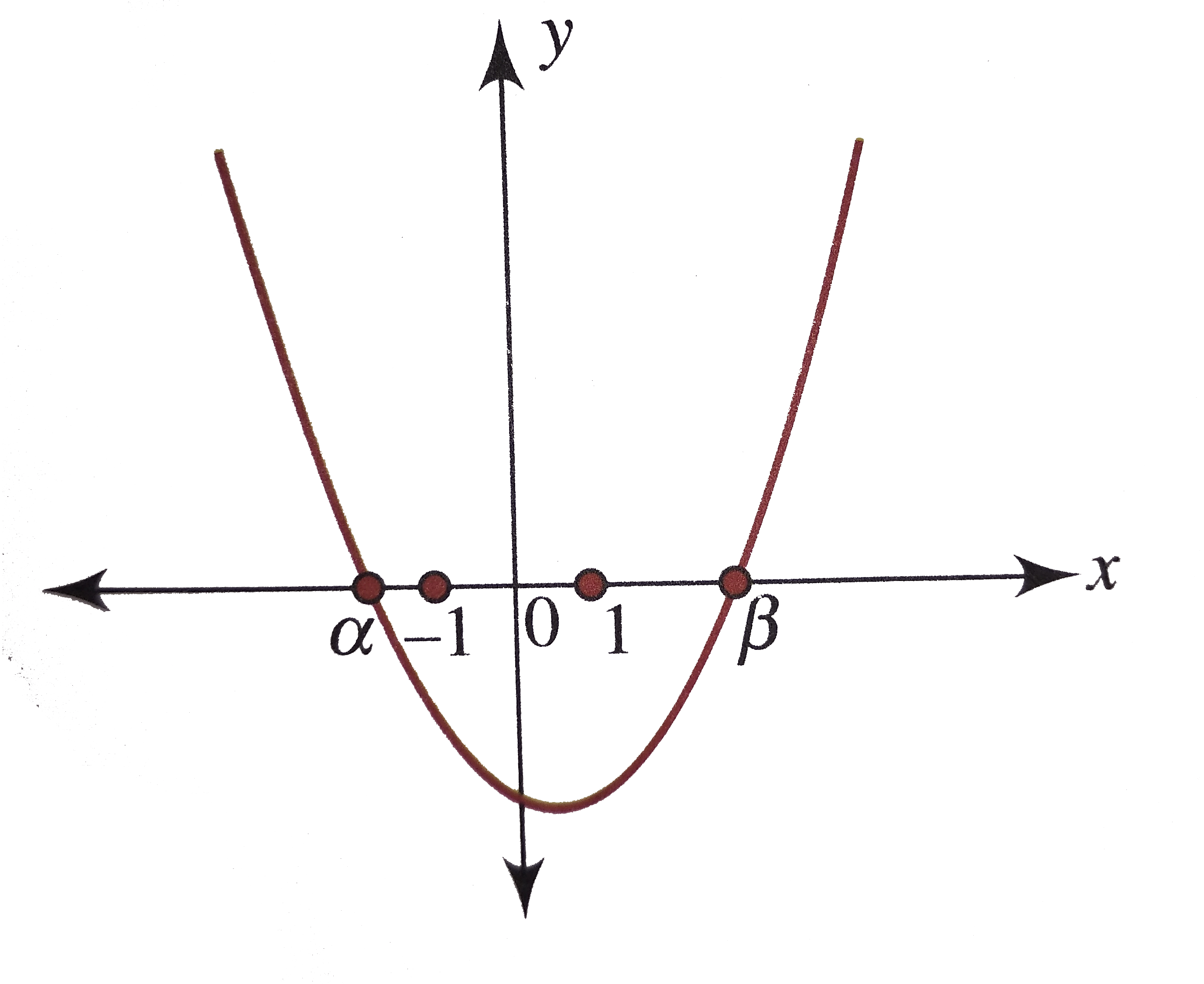
From the graph
f(−1)<0andf(1)<0
⇒ 1+ca−ba<0and1+ca+ba<0
⇒ 1+ca+∣∣∣ba∣∣∣<0
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLet a,b,c be real. If ax2+bx+c=0 has two real roots α and β, where α⟨−1 and β⟩1, then show that 1+ca+∣∣∣ba∣∣∣<0
View Solutionax^(2)+bx+c=0 has real and distinct roots alpha and beta(beta>alpha) .further a>0,b<0,c<0 then
View SolutionIf alpha,beta are non-real roots of ax^(2)+bx+c=0,(a,b,c in R), then (A)alpha beta=1(B)alpha=beta(C)(a beta)/(alpha beta)=1(D)alpha=bar(beta)
View SolutionLet a,b,c be real if ax2+bx+c=0 has two real roots α and β where a<−2 and β>2, then
View Solutionमाना a,b,c वास्तविक है| यदि ax2+bx+c=0 के दो वास्तविक मूल α और β है, जहाँ α<−1 और β>1, तब दिखाए कि
1+ca+∣∣∣ba∣∣∣<0
View SolutionLet a, b, c be real, if ax2+bx+c=0 has two real roots α,β, where a<−1andβ>1, then the value of 1+ca+∣∣∣ba∣∣∣ is :
View SolutionIf a, b, c are real if ax2+bx+c=0 has two real roots α,β where a<−1,β>1 then
View SolutionIf α and β(α<β) are two different real roots of the equation ax2+bx+c=0 then
View SolutionIf α and β (α<β) are two different real roots of the equation
ax2+bx+c=0, then
View SolutionLet a, b, c be real, if ax2+bx+c=0 has two real roots α,β, where a<−1andβ>1, then the value of 1+ca+∣∣∣ba∣∣∣ is :
View SolutionLet a, b, c be real, if ax2+bx+c=0 has two real roots α,β, where a<−1andβ>1, then the value of 1+ca+∣∣∣ba∣∣∣ is :
View SolutionLet a, b, c be real. If ax2+bx+c=0 has two real roots α and β such that α<−1 and β>1, then 1+ca+∣∣∣ba∣∣∣is
View SolutionIf 0<a<b<c and the roots α,β of the equation ax2+bx+c=0 are non-real complex numbers, then
View Solution
