Let f(x)=2x(2−x),0≤x≤2. Then find the number of solutions of f(f(f(x)))=x2. Solution in Tamil
We have f(x)=2x(2−x),0≤x≤2
The graph of y=f(x) is parabola, which is concave downwards as shown in the following figure.
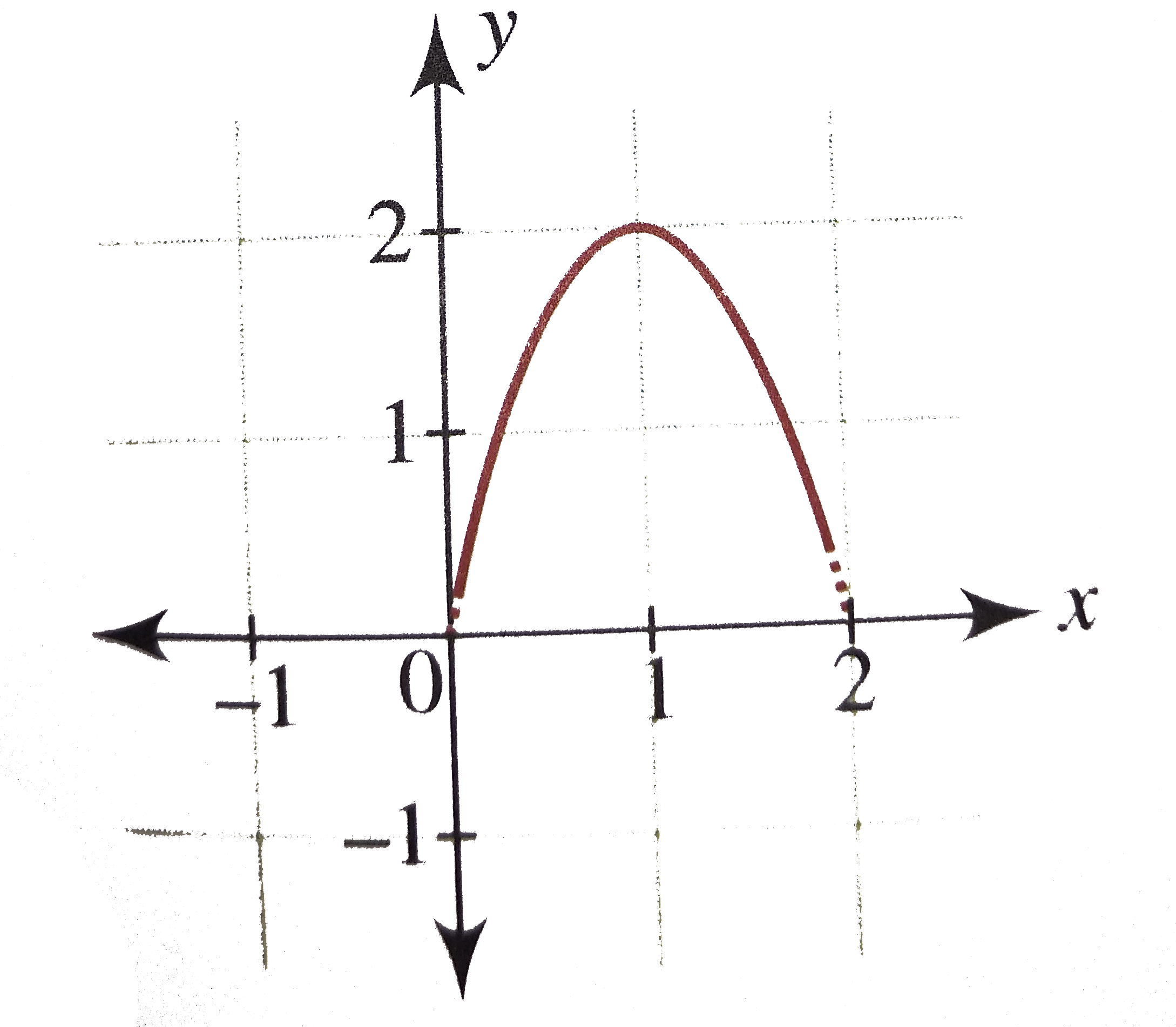
Range of y=f(x) is [ 0, 2 ].
Now f(f(x))=2f(x)(2−f(x)), which is a fourth degree polynomial function.
f(f(x))=0theref0ref(x)=0orf(x)=2
∴ x=0,2or2x(2−x)=2
∴ x=0,1,1,2
Thus, f(f(x))=0 has four roots in which one root is repeated.
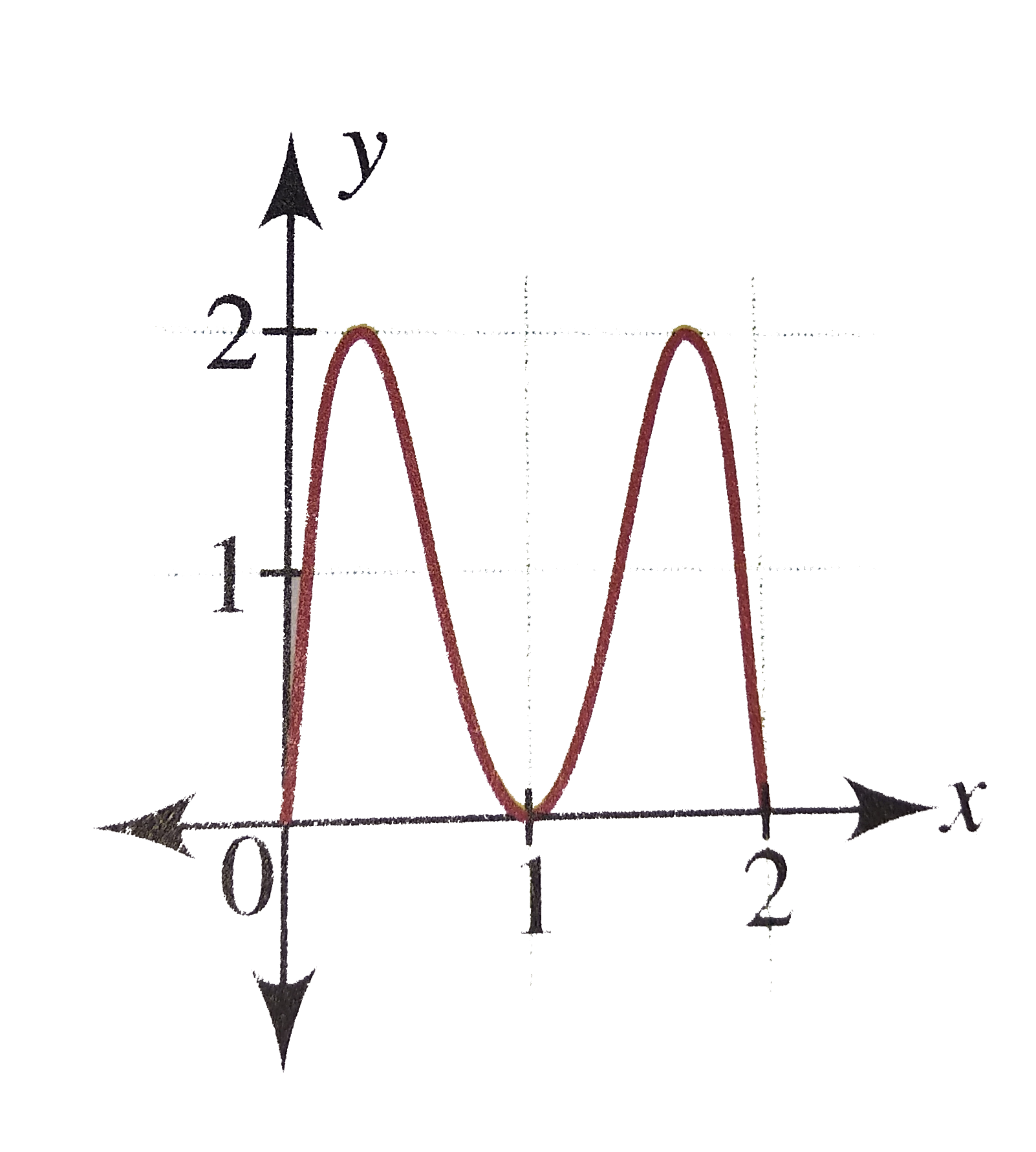
Also the range of y=f(f(x)) is [0, 2] as f(x)∈ [0, 2] for x∈ [0, 2].
So the graph of y=f(f(x)) is
With similar arguments, the graph of y=f(f(f(x))) is as follows :
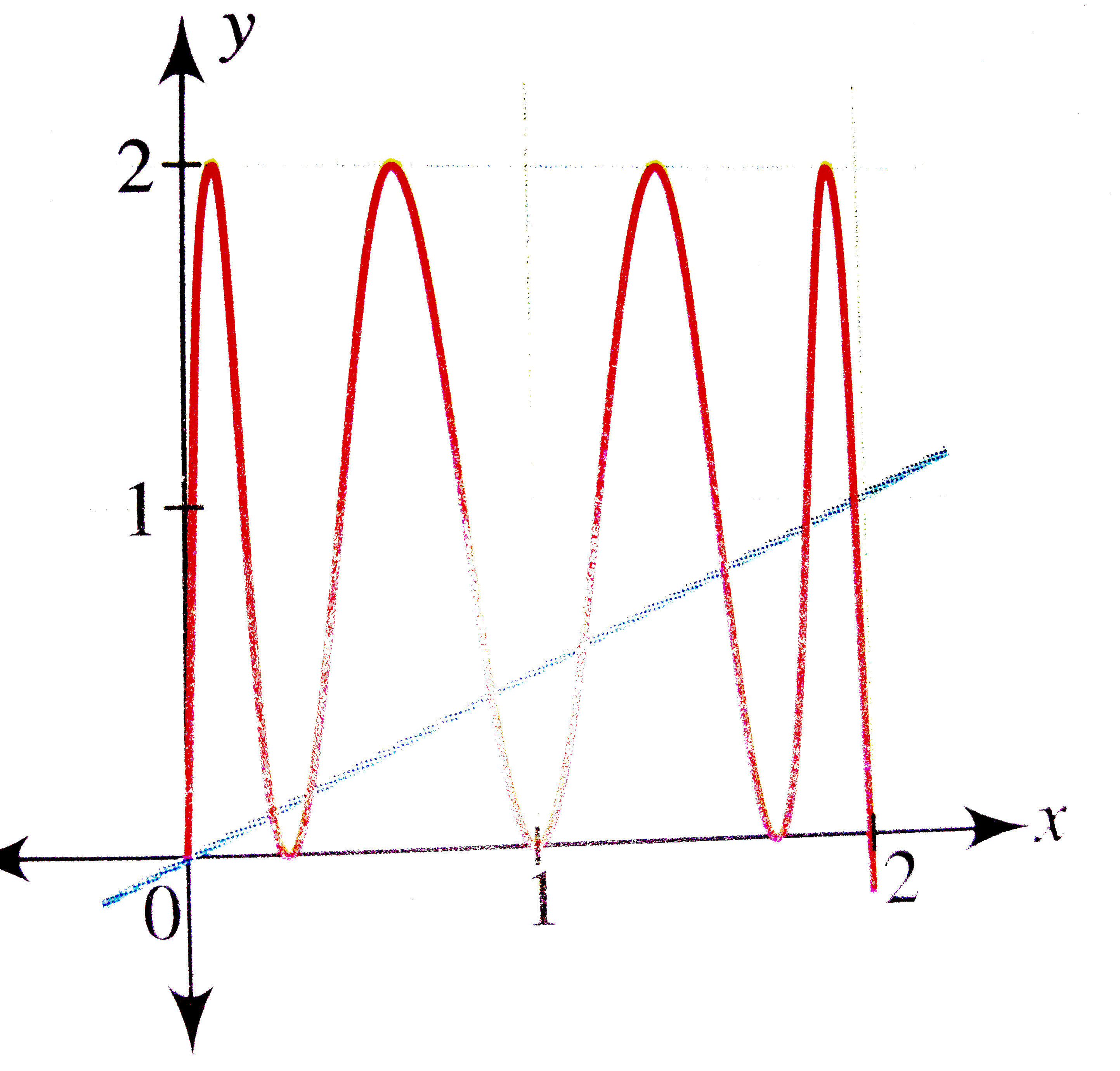
Clearly, the line y=x/2 meets the graph of y=f(f(x)) in eight points, hence '8' roots.
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLet f(x)=2x(2−x),0≤x≤2. Then find the number of solutions of f(f(f(x)))=x2.
View SolutionLet f(x)=x(2−x),0≤x≤2. If the definition of f(x) is extended over the set R−[0,2] by f(x+1)=f(x), then f is a
View SolutionSuppose f:[−2,2]→R is defined by f(x)={−1 for −2≤x≤0x−1 for 0≤x≤2 , then {x∈[−2,2]:x≤0andf(|x|)=x}=
View SolutionIf f(x)={1+x0≤x≤23x−22<x≤3, then f(f(x)) is not differentiable at:
View SolutionLet f(x)={−1−2≤x<0x2−10≤x≤2 and g(x)=|f(x)|+f(|x|). Then , in the interval (-2,2),g is
View SolutionLet the function f be defined by
f(x)=|x−1|−12,0≤x≤2,f(x+2)=f(x) for all x∈R.
Evaluate (i)∫1000f(x)dx
(ii) ∫10|f(2x)|dx
View Solutionf(x)={(x,0,≤,x,≤,2),(3x,−,1,2,<,x,≤,3) then f'(2+) is:
View Solutionf(x)={(x,0,≤,x,≤,1),(2x,−,1,1,<,x,≤,2) then f'(1−) is :
View Solutionf(x)={2x−30≤x≤2x2−32≤x≤4 then f'(2+) and f'(2−) are:
View Solutionf(x)=x2+1,0≤x≤2
find the range of the function f.
View SolutionLet f(x)=2x(2−x),0≤x≤2. Then find the number of solutions of f(f(f(x)))=x2.
View Solutionमाना एक फलन f(x)=⎡⎢⎣1−x0≤x≤1x+21<x<24−x2≤x≤4 हो तो f(f(x))" और "underset(x to 2)Lim f(f(x)) का मान ज्ञात कीजिये
View SolutionLet f(x)=x(2−x),0≤x≤2. If the definition of 'f' is extended over the set R−[0,2] by f(x+1)=f(x) then f is a periodic function with period.
View Solution
