A tower of height b subtends an angle α at a point on the same level as the food of the tower .At a second point , b meters above the first , the angle of depression of the foot pole and the finds that the elevation is now 2θ .The value of cot θ is Solution in Tamil
b cot α tan β
btanαtanβ
btanαcotβ
bcotαcotβ
Let AB be the tower of height h, D be the point x away fron B and C be another point b m above D
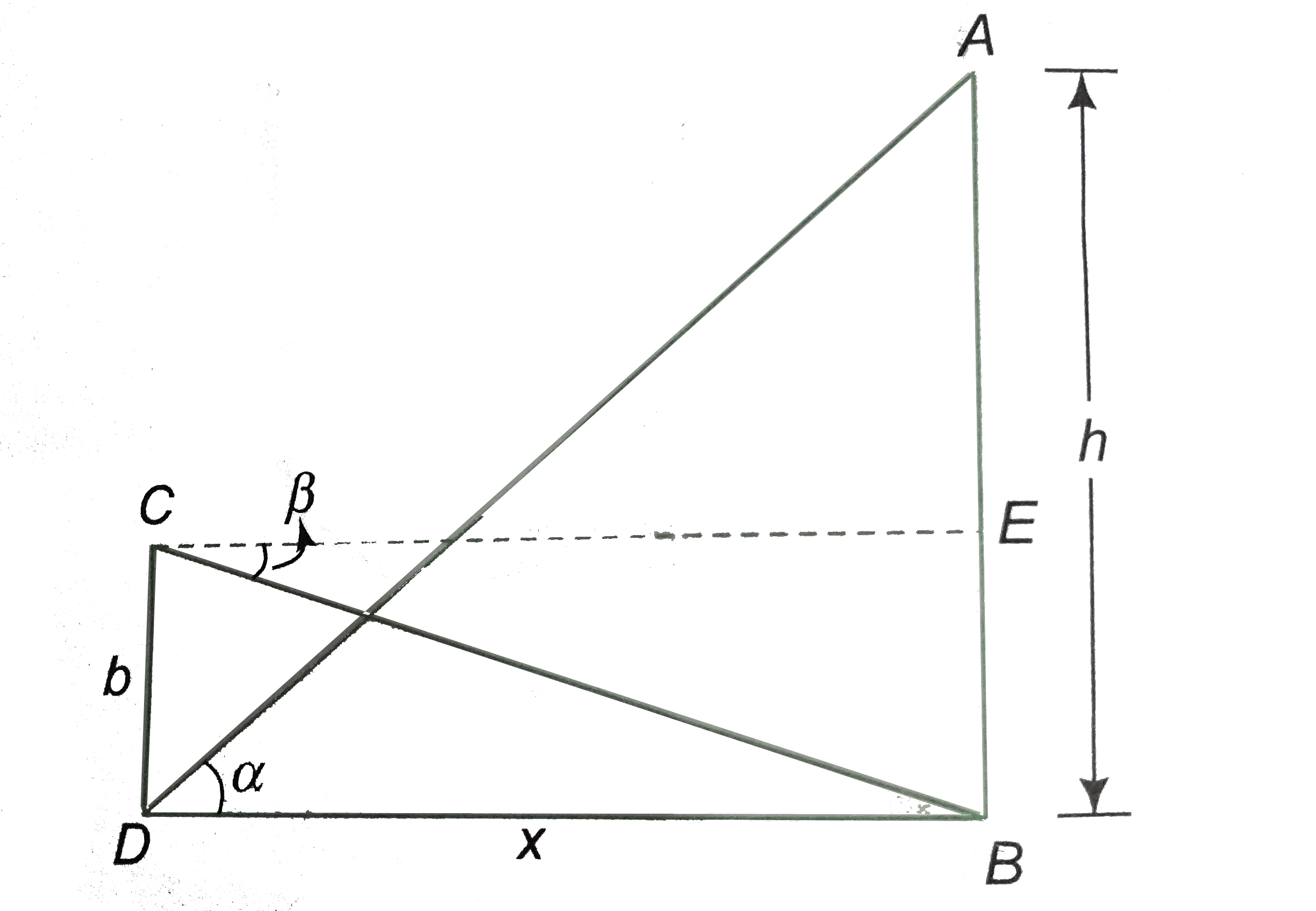
In triangle ABD.
h=xtanα
In triangle BCE. X=bcotβ
from (1) and (2) we get
∴h=btanαcotβ
Topper's Solved these Questions
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- HYPERBOLABOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year
14 Videos
Similar Questions
A bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLet P(6,3) be a point on the hyperbola x2a2−y2b2=1. If the normal at point P intersects the x-axis at (9, 0), then find the eccentricity of the hyperbola.
View SolutionA tower of height b subtends an angle α at a point on the same level as the food of the tower .At a second point , b meters above the first , the angle of depression of the foot pole and the finds that the elevation is now 2θ .The value of cot θ is
View SolutionA tower subtends an angle alpha at a point in the plane of its base and the angle of depression of the foot of the tower at a point b ft. just above A is beta . Then , height of the tower is
View SolutionA tower subtends an angle of 30^@ at a point on the same level as the foot of the tower. At a second point h meter above the first, the depression of the foot of the tower is 60^@ . The horizontal distance of the tower from the point is
View SolutionThe electric pole subtends an angle of 30^(@) at a point on the same level as its foot. At a second point 'b' metres above the first, the depression of the foot of the tower is 60^(@) . The height of the tower (in towers) is equal to
View SolutionA tower subtends an angle of 60∘ at a point on the same level as the foot of the tower and at a second point just 10 meters above the first point the angle of depression of the foot of the tower is 15∘. The height of the tower is (in meters)
View SolutionA tower subtends an angle α at a point A in the plane of its base and the angle of depression of the foot of the tower at a point b ft just above A is β. Then the height of the tower is
View SolutionA tower subtends an angle 75∘ at a point on the same level as the foot of the tower and at another point, 10 meters above the first, the angle of depression of the foot of the tower is 15∘. The height of the tower is (in meters)
View SolutionA tower subtends an angle alpha at a point on the same level as the foot of the tower and at the second point h metres above the first the angle of depression of the base of a tower is beta The height of the tower
View SolutionA tower subtends an angle α at a point A in the plane of its base and the angle of depression of the foot of the tower at a point b ft hust above A is β . Then the height of the tower is
View SolutionA tower subtends an angle α at a point on the same level as the root of the tower and at a second point, b meters above the first, the angle of depression of the foot of the tower is β. The height of the tower is
View SolutionA tower subtends an angle α at a point A on the same level as the foot of the tower B is a point vertically above A and AB = h metres. The angle of depression of the foot of the tower from B is β. The height of the tower is
View Solution
