A ladder rest against a wall making an angle α with the horizontal. The foot of the ladder is pulled away from the wall through a distance x, so that it slides a distance y down the wall making an angle β with the horizontal. Prove that x=ytan(α+β)2.Solution in Tamil
y=xtanα+β2
x=ytanα+β2
x=ytan(α+β)
y=xtan(α+β)
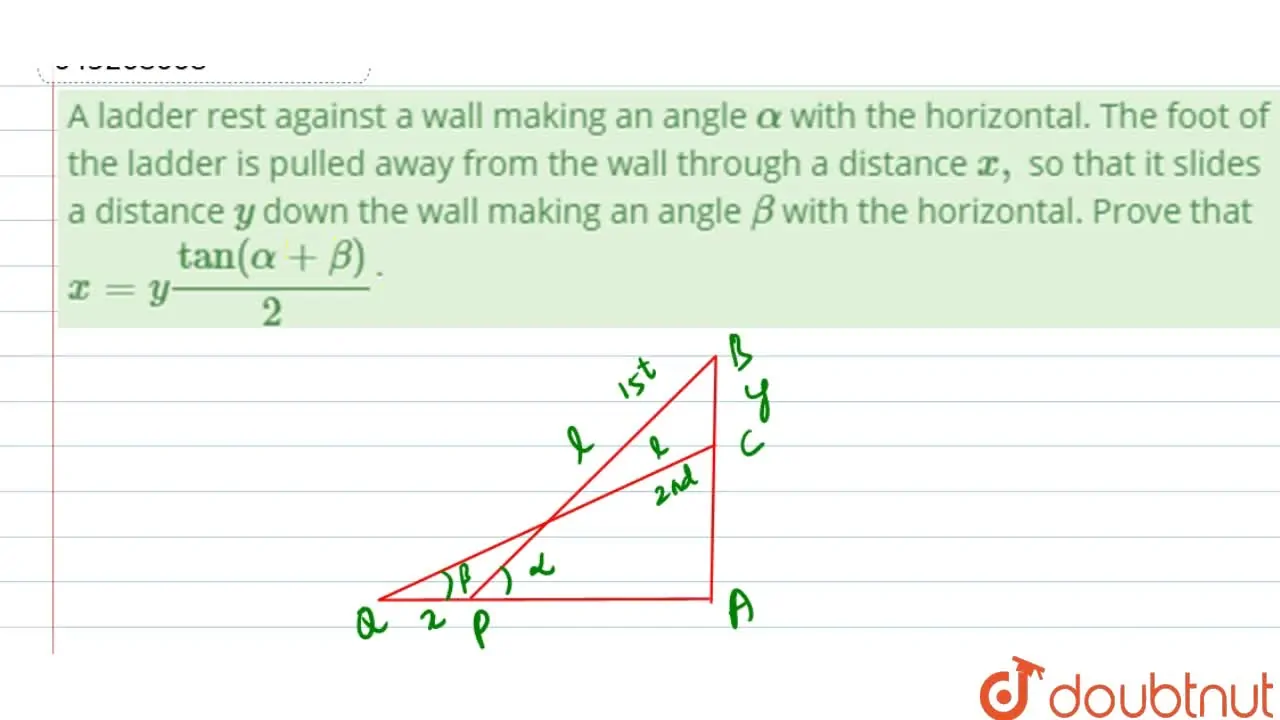
Let AB be the wall, P be the intial position and Q be the final position of the foot of the ladder on the ground
 In the figure , PB =QC =1
In the figure , PB =QC =1
In triangle BAP,PA = l cos α AB= li sin α
In triangle CAQ , QA = l cos β , AC l sin β
Now y=BC=AB−AC=(sinα−sinβ)
and =x=PQ=AQ−AP=l(cosβ−cosα)
⇒yx=sinα−sinβcosβ−cosα
2sin(α−β2)cos(α+β2)2sin(α+β2)cos(α−β2)
⇒yx=cot(α+β2)
⇒yx=cot(α+β2)
⇒x=ytan(α+β2)
Related Playlists
- BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year3videos
HIGHT AND DISTANCE
- BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year3videos
HIGHT AND DISTANCE
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year14videos
HYPERBOLA
Similar Questions
A bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
04:21View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
05:40View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
04:45View SolutionLet P(6,3) be a point on the hyperbola x2a2−y2b2=1. If the normal at point P intersects the x-axis at (9, 0), then find the eccentricity of the hyperbola.
09:13View SolutionA ladder rests against a vertical wall at inclination alpha to the horizontal.Its foot is pulled away from the wall through a distance p so that it's upper end slides q down the wall and then ladder make an angle beta to the horizontal show that (p)/(q)=(cos beta-cos alpha)/(sin alpha-sin beta)
06:07View Solutionladder rests against a wall at an angle alpha to the horizontal its foot pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle beta with the horizontal.Show that (a)/(b)=(cos alpha-cos beta)/(sin beta-sin alpha)
03:51View SolutionA ladder rest against a wall making an angle α with the horizontal. The foot of the ladder is pulled away from the wall through a distance x, so that it slides a distance y down the wall making an angle β with the horizontal. Prove that x=ytan(α+β)2.
03:51View SolutionA ladder rests against a wall making an angle α with the horizontal. The foot of the ladder is pulled away from the wall through a distance x, so that it slids a distance y down the wall making an angle β with the horizontal. Then prove that
x=ytan(α+β2).05:32View SolutionA ladder rests against a vertical wall at angle α to the horizontal . If is foot is pulled away from the wall through a distance 'a' so that it slides a distance 'b' down the wall making the angle β with the horizontal , then a =
05:42View SolutionA ladder rests against a wall making an angle alpha with the horizontal. The foot of the ladder is pulled away from the wall through a distance x so that it slides a distance y down the wall making an angle beta with the horizontal.The correct relation is (A) x=y tan(alpha+beta)/(2) (B) y=x tan(Q+beta)/(2) (c) x=y tan(alpha+beta) (0) y=x tan(alpha+beta) (a)
08:40View SolutionA ladder rests against a wall making an angle alpha with the horizontal. The foot of the ladder is pulled away from the wall through a distance x so that it slides a distance y down the wall making an angle beta with the horizontal.The correct relation is (A) x=y tan(alpha+beta)/(2) (B) y=x tan(alpha+beta)/(2) (C) x=y tan(alpha+beta) (D) y=x tan(alpha+beta) (in)
08:16View SolutionA ladder rests against a wall at an angle alpha to the horizontal, its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle beta with the horizontal. Show that a = b tan 1/2(alpha + beta) .
05:56View SolutionA ladder rests against a vertical wall at an angle α to the horizontal. If the foot is pulled away through a distance 2m, then it slides a distance 5 m down the wall, finally making an angle β with the horizontal. The value of tan(α+β2) is equal to
07:23View SolutionA ladder rest against a wall making an angle α with the horizontal. The foot of the ladder is pulled away from the wall through a distance x, so that it slides a distance y down the wall making an angle β with the horizontal. Prove that x=ytan(α+β)2.
05:02View SolutionA ladder rest against a wall making an angle α with the horizontal. The foot of the ladder is pulled away from the wall through a distance x, so that it slides a distance y down the wall making an angle β with the horizontal. THEN x=
05:59View SolutionA ladder rests against a wall at an angle alpha to the horizontal. Its foot is pulled away from the wall through a distance 'a' so that it slides a distance 'b' down the wall making an angle beta with the horizontal. Show that: a=b tan(1/2(α+β)) .
03:26View Solution