A man fires a bullet of mas 20g at a speed of 100 m/s. The gun is 2 kg mass. By what velocity the gun rebounds backward?
2 m/s
1 m/s
5 m/s
6 m/s
The correct Answer is:B
To solve the problem of the gun's recoil velocity when a bullet is fired, we will use the principle of conservation of momentum. Here are the steps to find the solution:
1. Identify the Given Data:
- Mass of the bullet (m_bullet) = 20 g = 0.02 kg (conversion from grams to kilograms)
- Speed of the bullet (v_bullet) = 100 m/s
- Mass of the gun (m_gun) = 2 kg
2. Understand the Conservation of Momentum:
According to the law of conservation of momentum, the total momentum before firing the bullet is equal to the total momentum after firing the bullet. Initially, both the gun and bullet are at rest, so the initial momentum is zero.
Initial momentum=0
After firing, the momentum of the bullet and the gun can be expressed as:
Final momentum=mbullet⋅vbullet+mgun⋅vgun
Where vgun is the recoil velocity of the gun that we need to find.
3. Set Up the Equation:
Since the initial momentum is zero, we can write:
0=mbullet⋅vbullet+mgun⋅vgun
Rearranging the equation gives:
mgun⋅vgun=−mbullet⋅vbullet
4. Substitute the Known Values:
Plugging in the values we have:
2⋅vgun=−(0.02⋅100)
This simplifies to:
2⋅vgun=−2
5. Solve for vgun:
Dividing both sides by 2:
vgun=−1 m/s
The negative sign indicates that the gun moves in the opposite direction to the bullet.
Final Answer:
The recoil velocity of the gun is 1 m/s backward.
---
- Mass of the bullet (m_bullet) = 20 g = 0.02 kg (conversion from grams to kilograms)
- Speed of the bullet (v_bullet) = 100 m/s
- Mass of the gun (m_gun) = 2 kg
According to the law of conservation of momentum, the total momentum before firing the bullet is equal to the total momentum after firing the bullet. Initially, both the gun and bullet are at rest, so the initial momentum is zero.
Final momentum=mbullet⋅vbullet+mgun⋅vgun
Since the initial momentum is zero, we can write:
0=mbullet⋅vbullet+mgun⋅vgun
mgun⋅vgun=−mbullet⋅vbullet
Plugging in the values we have:
2⋅vgun=−(0.02⋅100)
2⋅vgun=−2
Dividing both sides by 2:
vgun=−1 m/s
The recoil velocity of the gun is 1 m/s backward.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - PHYSICS WALLAHCHAPTER - LAWS OF MOTION EXERCISE - LEVEL-2
18 Videos
- LAWS OF MOTION BOOK - PHYSICS WALLAHCHAPTER - LAWS OF MOTION EXERCISE - NEET PAST 5 YEARS QUESTIONS
12 Videos
- KINETIC THEORY BOOK - PHYSICS WALLAHCHAPTER - KINETIC THEORY EXERCISE - NEET PAST 5 YEARS QUESTIONS
11 Videos
- MAGNETISM AND MATTER BOOK - PHYSICS WALLAHCHAPTER - MAGNETISM AND MATTER EXERCISE - NEET PAST 5 YEARS QUESTIONS
10 Videos
Similar Questions
A bullet of mass 50kg is fired with a speed of 200m/s from a gun of mass 2kg . Find the recoil velocity of the gun.
View SolutionA machine gun fires a bullet of mass 65 g with a velocity of 1300 m/s. The man holding it can exert a maximum force of 169 N on the gun. The number of bullets he can fire per second will be
View Solution
Knowledge Check
A man fires a bullet of mass 200 g at a speed of 5 m/s . The gun is of one kg mass. By what velocity the gun rebounds backwards
A0.1m/sB10m/sC1m/sD0.01m/sA bullet of mass 0.1 kg is fired with a speed of 100 m/sec , the mass of gun is 50 kg . The velocity of recoil is
A0.2m/secB0.1m/secC0.5m/secD0.05m/secA gun fires a bullet of mass 50g with a velociy of 30m/s. Due to this, the gun is pushed back with a velocity of 1m/s, then the mass of the gun is :
A1.5kgB5.5kgC0.5kgD3.5kg
A gun of mass 4 kg initially at rest fires a bullet of mass 4g with a speed of 50m/s as seen by an observer on ground. Find the impulse on bullet and recoil speed of the gun.
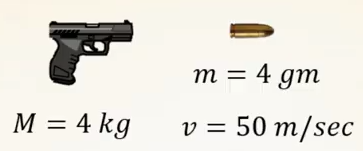
View SolutionA 60 g bullet fired from a 5 kg gun leaves with a speed of 500 m/s. Find the speed (velocity) with which the gun recoils (jerks backwards).
View SolutionA gun weighing 10 kg fires a bullet of 30 g with a velocity of 330 ms−1 . With what velocity does the gun recoil? What is the combined momentum of the gun and bullet before firing and after firing?
View SolutionA bullet of mass 0.1 kg is fired with a speed of 100ms−1. The mass of gun being 50 kg. Then, the velocity of recoil becomes
View SolutionA machine gun fires a bullet of mass 65 g with a velocity of 1300 m/s. The main holding it can exert a maximum force of 169 N on the gun. The number of bullets he can fire per second will be
View Solution
