A man fires a bullet of mass 200 g at a speed of 5 m/s . The gun is of one kg mass. By what velocity the gun rebounds backwards
0.1m/s
10m/s
1m/s
0.01m/s
The correct Answer is:C
To solve the problem of the gun's recoil when a bullet is fired, we can use the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Understand the System
When the bullet is fired, the system consists of the bullet and the gun. Initially, both the bullet and the gun are at rest, so the total initial momentum of the system is zero.
Step 2: Define the Masses
- Mass of the bullet, mb=200g=0.2kg (since 1 g = 0.001 kg)
- Mass of the gun, mg=1kg
Step 3: Define the Speeds
- Speed of the bullet after firing, vb=5m/s
- Let the recoil speed of the gun be vg (this will be a negative value since it moves in the opposite direction of the bullet).
Step 4: Apply Conservation of Momentum
According to the conservation of momentum:
Initial Momentum=Final Momentum
Since the initial momentum is zero, we have:
0=mb⋅vb+mg⋅vg
Step 5: Substitute the Values
Substituting the known values into the equation:
0=(0.2kg)⋅(5m/s)+(1kg)⋅vg
Step 6: Solve for vg
Rearranging the equation gives:
(1kg)⋅vg=−(0.2kg)⋅(5m/s)
vg=−(0.2⋅5)1
vg=−1m/s
Conclusion
The gun rebounds backwards with a velocity of 1m/s.
---
When the bullet is fired, the system consists of the bullet and the gun. Initially, both the bullet and the gun are at rest, so the total initial momentum of the system is zero.
- Mass of the bullet, mb=200g=0.2kg (since 1 g = 0.001 kg)
- Mass of the gun, mg=1kg
- Speed of the bullet after firing, vb=5m/s
- Let the recoil speed of the gun be vg (this will be a negative value since it moves in the opposite direction of the bullet).
According to the conservation of momentum:
Initial Momentum=Final Momentum
Since the initial momentum is zero, we have:
0=mb⋅vb+mg⋅vg
Substituting the known values into the equation:
0=(0.2kg)⋅(5m/s)+(1kg)⋅vg
Rearranging the equation gives:
(1kg)⋅vg=−(0.2kg)⋅(5m/s)
vg=−(0.2⋅5)1
vg=−1m/s
The gun rebounds backwards with a velocity of 1m/s.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ERRORLESS Chapter:NEWTONS LAWS OF MOTIONExercise:Equilibrium of Force
Explore 18 Videos
- NEWTONS LAWS OF MOTIONBook:ERRORLESS Chapter:NEWTONS LAWS OF MOTIONExercise:Motion of Connected Bodies
Explore 23 Videos
- NEWTONS LAWS OF MOTIONBook:ERRORLESS Chapter:NEWTONS LAWS OF MOTIONExercise:Third Law of Motion
Explore 24 Videos
- MOTION IN TWO DIMENSIONBook:ERRORLESS Chapter:MOTION IN TWO DIMENSIONExercise:Exercise
Explore 319 Videos
- ROTATIONAL MOTIONBook:ERRORLESS Chapter:ROTATIONAL MOTIONExercise:Practice Problems (Problems based on motion of connected mass)
Explore 10 Videos
Similar Questions
Knowledge Check
A man fires a bullet of mas 20g at a speed of 100 m/s. The gun is 2 kg mass. By what velocity the gun rebounds backward?
A2 m/sB1 m/sC5 m/sD6 m/sA bullet of mass 0.1 kg is fired with a speed of 100 m/sec , the mass of gun is 50 kg . The velocity of recoil is
A0.2m/secB0.1m/secC0.5m/secD0.05m/secA gun fires a bullet of mass 50g with a velociy of 30m/s. Due to this, the gun is pushed back with a velocity of 1m/s, then the mass of the gun is :
A1.5kgB5.5kgC0.5kgD3.5kg
A gun fires a bullet of mass 50 g with a velocity of 30 m s−1 because of which the gun recoils with a velocity 1 m s−1. Find the mass of the gun.
View SolutionA gun of mass 4 kg initially at rest fires a bullet of mass 4g with a speed of 50m/s as seen by an observer on ground. Find the impulse on bullet and recoil speed of the gun.
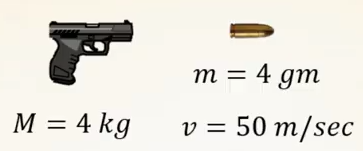
View SolutionA bullet of mass 0.1 kg is fired with a speed of 100ms−1. The mass of gun being 50 kg. Then, the velocity of recoil becomes
View SolutionA bullet of mass 50 gram is fired from a 5 kg gun with a velocity of 1 km/s . the speed of recoil of the gun is
View SolutionA bullet of mass 10 g is fired with a velocity of 20 m/s from a gun of mass 2 kg. Find the recoil velocity (in m/s) of the gun.
View Solution

