A block of mass 10 kg in contact against the inner wall of a hollow cylindrical drum of radius 1m. The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be (g=10m/s2)
√10rad/s
102πrad/s
10 rad/s
10π rad/s
The correct Answer is:C
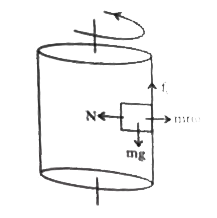
For equilibrium of the block limiting friction f1≥mg
⇒μN≥mg
⇒μmrω2≥mg
m≥√grμ
Therefore,
mmin=√grμ
ωmax=√100.1×1=10 rad/s
Topper's Solved these Questions
- LAWS OF MOTION BOOK - PHYSICS WALLAHCHAPTER - LAWS OF MOTION EXERCISE - LEVEL-2
18 Videos
- KINETIC THEORY BOOK - PHYSICS WALLAHCHAPTER - KINETIC THEORY EXERCISE - NEET PAST 5 YEARS QUESTIONS
11 Videos
- MAGNETISM AND MATTER BOOK - PHYSICS WALLAHCHAPTER - MAGNETISM AND MATTER EXERCISE - NEET PAST 5 YEARS QUESTIONS
10 Videos
Similar Questions
A person stands in contact against the inner wall of a rotor of radius r. The coefficient of friction between the wall and the clothing is μ and the rotor is rotating about vertical axis. The minimum angular speed of the rotor so that the person does not slip downward is
View SolutionA 70kg man stands in contact against the inner wall of a hollw cylindrical drum of radius 3m rotating about its verticle axis. The coefficient of friction between the wall and his clothing nis 0.15 . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
View Solution
Knowledge Check
A block of mass 10 kg in contact against the inner wall of a hollow cylindrical drum of radius 1m. The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be (g=10m/s2)
A√10rad/sB102πrad/sC10 rad/sD10π rad/sA block of mass 10 kg is in contact against the inner wall of a hollow cylindrical drum of radius 1 m. The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be (g=10m/s2)
A10πrad/sB√10rad/sC102πrad/sD10rad/sIn a 'well of death' a ride drives round the inner wall of a hollow cylindrical chamber of siameter 20 m .If the coefficient of force friction between tyres and inner wall of a hollow cylinder is 0.5, then the minimum speed of the rider without sliding down will be
A7m/sB14m/sC2√7m/sD7√2m/s
A block of mass 1kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5 ,magnitude of the frictional force acting on the block is
View SolutionA block of mass 0.1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, then the magnitude of the frictional force acting on the block is
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionA horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
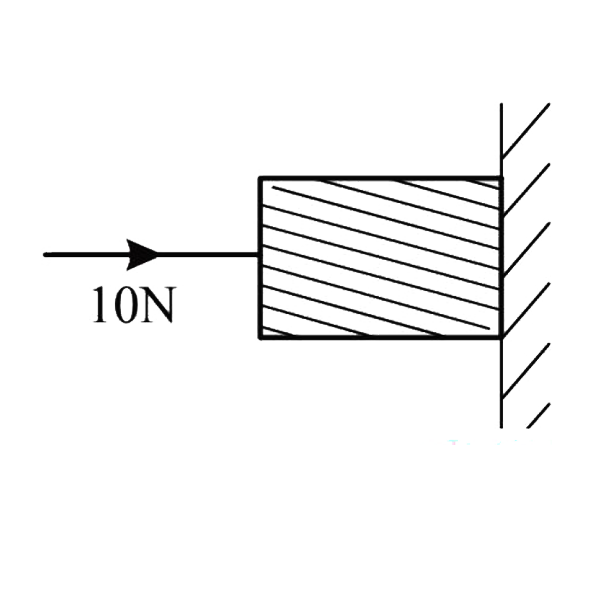
View SolutionA horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is

View Solution
