A source emits a sound of frequency of 400 Hz , but the listener hears it to be 390 Hz . Then
The listener is moving towards the source
The source is moving towards the listener
The listener is moving away from the source
The listener has a defective ear
The correct Answer is:C
To solve the problem, we need to determine the motion of the source and the listener based on the frequencies given. The source emits a sound of frequency f=400Hz, and the listener hears it as f′=390Hz.
1. Understanding the Doppler Effect: The Doppler effect describes how the frequency of a wave changes for an observer moving relative to the source of the wave. If the observer is moving towards the source, the frequency heard by the observer increases. Conversely, if the observer is moving away from the source, the frequency decreases.
2. Identifying the Frequencies: In this case, the actual frequency emitted by the source is f=400Hz, and the apparent frequency heard by the listener is f′=390Hz. Since f′<f, it indicates that the listener is moving away from the source.
3. Applying the Doppler Effect Formula: The formula for the apparent frequency when the observer is moving away from a stationary source is given by:
f′=f(vv+vo)
where:
- f′ = apparent frequency (390 Hz)
- f = actual frequency (400 Hz)
- v = speed of sound in air (approximately 343m/s at room temperature)
- vo = speed of the observer (which we need to find)
4. Rearranging the Formula: We can rearrange the formula to solve for vo:
vo=v(ff′−1)
5. Substituting the Values: Now we substitute the known values into the equation:
vo=343(400390−1)
6. Calculating the Value:
vo=343(1.0256−1)=343×0.0256≈8.77m/s
7. Conclusion: The speed of the observer moving away from the source is approximately 8.77m/s.
f′=f(vv+vo)
where:
- f′ = apparent frequency (390 Hz)
- f = actual frequency (400 Hz)
- v = speed of sound in air (approximately 343m/s at room temperature)
- vo = speed of the observer (which we need to find)
vo=v(ff′−1)
vo=343(400390−1)
vo=343(1.0256−1)=343×0.0256≈8.77m/s
Similar Questions
A source emits sound of frequency 600Hz inside water. The frequency heard in air will be equal to (velocity of sound in water=1500ms, velocity of sound in air=300(m)/(s))
View SolutionA sound detector is moving with a constant velocity towards a stationary sound source. The source emits a beep of sound of frequency f=262 Hz that propogates with speec c=330m/s. The detector detects the beep of sound over a distance L=78 m and registers a frequency f=275 Hz. Find thhe duration of the beep emitted by the source.
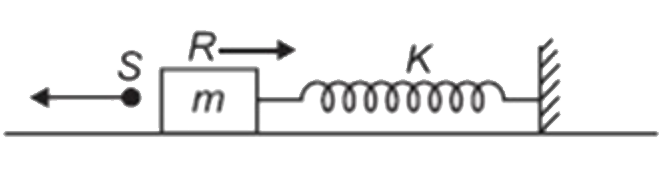
View SolutionA sound source S, emitting a sound of frequency 400 Hz and a receiver R of mass m are at the same point. R is performing SHM with the help of a spring of force constant K. At a time t = 0, R is at the mean position and moving towards the right, as shown. At the same time, the source starts moving away from R with some acceleration a. The frequency registered by the receiver at a time t = 10 s is 250 Hz. What is the time (in seconds) at which the corresponding registered frequency of 250 Hz was emitted by the source? [Given that mK=25π2 and amplitude of oscillation = 100πm,Vsound = 320 m s^(-1)]
 View Solution
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionA stationary source emits sound of frequency 1200 Hz. If would blows at the speed of 0.1 v. deduce
(a) The change in the frequency for a stationary observer on the wind side of the source
(b) Report the calculations for the case when there is no wind but the observer moves at 0.1 v speed towards the source (Given : velocity of sound = v)View SolutionA source is moving with a constant speed of 10 m/s on a circular track of 200 m. It emits a sound of frequency 200 Hz. A listener stands at the centre of the circular track. The frequency received by the listener is (velocity of sound = 340 m/s)
View SolutionA stationary source emits sound of frequency
υ=1200Hz. If a wind blows at the speed of 0.1c deduce (i) the percentage change in the wavelength and (ii) the change in the frequency for a stationary observer on the wind side of the source. What happens when there is no wind, but the observer moves at speed 0.1c towards the source?View SolutionA stationary source emits sound of frequency
υ=1200Hz. If a wind blows at the speed of 0.1c deduce (i) the percentage change in the wavelength and (ii) the change in the frequency for a stationary observer on the wind side of the source. What happens when there is no wind, but the observer moves at speed 0.1c towards the source?View SolutionA stationary source emits the sound of frequency f0=492 Hz. The sound is reflected by a large car approaching the source with a speed of 2ms−1. The reflected signal is received by the source and superposed with the original. What will be the beat frequency of the resulting signal in Hz? (Given that the speed of sound in air is 330ms−1 and the car reflects the sound at the frequency it has received).
View SolutionA plice siren emits a sound wave of frequency 440 Hz. The speed of sound is 332 m/s. if the siren is moving away from the listerner with a speed of 18 m/s relative to the air and the listerner is moving towards the siren with a speed of 68 m/s relative to the air, then what frequency does the listern hear?
View Solution
