A sound detector is moving with a constant velocity towards a stationary sound source. The source emits a beep of sound of frequency f=262 Hz that propogates with speec c=330m/s. The detector detects the beep of sound over a distance L=78 m and registers a frequency f=275 Hz. Find thhe duration of the beep emitted by the source.
2s
4s
5s
6s
The correct Answer is:C
To solve the problem, we need to find the duration of the beep emitted by the sound source. We will use the relationship between the frequencies and the speed of sound to derive the duration.
1. Identify the Given Values:
- Frequency of the source, f0=262Hz
- Speed of sound, c=330m/s
- Frequency detected by the moving detector, f=275Hz
- Distance over which the beep is detected, L=78m
2. Understand the Relationship Between Frequencies:
The relationship between the emitted frequency f0 and the observed frequency f when the detector is moving towards the source is given by:
f=c+v0cf0
where v0 is the velocity of the detector.
3. Rearranging the Equation:
We can rearrange the equation to find v0:
v0=c(ff0−1)
4. Substituting the Values:
Substitute f=275Hz and f0=262Hz:
v0=330(275262−1)
5. Calculating v0:
v0=330(1.049−1)=330×0.049≈16.17m/s
6. Finding the Duration of the Beep:
The duration of the beep can be calculated using the relationship:
t=Lv0
where L=78m.
7. Substituting the Values:
t=7816.17≈4.82s
8. Final Calculation:
Rounding off, we can say the duration of the beep is approximately t≈5s.
Conclusion:
The duration of the beep emitted by the source is approximately 5 seconds.
- Frequency of the source, f0=262Hz
- Speed of sound, c=330m/s
- Frequency detected by the moving detector, f=275Hz
- Distance over which the beep is detected, L=78m
The relationship between the emitted frequency f0 and the observed frequency f when the detector is moving towards the source is given by:
f=c+v0cf0
where v0 is the velocity of the detector.
We can rearrange the equation to find v0:
v0=c(ff0−1)
Substitute f=275Hz and f0=262Hz:
v0=330(275262−1)
v0=330(1.049−1)=330×0.049≈16.17m/s
The duration of the beep can be calculated using the relationship:
t=Lv0
where L=78m.
t=7816.17≈4.82s
Rounding off, we can say the duration of the beep is approximately t≈5s.
The duration of the beep emitted by the source is approximately 5 seconds.
Similar Questions
A source emits a sound of frequency of 400 Hz , but the listener hears it to be 390 Hz . Then
View SolutionA car is moving with a constant velocity 10m/s towards the stationary wall. The car blows a horn of frequency 320Hz. The velocity of sound in air is 330m/s. The beats frequency received by the observer is

View Solution
Knowledge Check
An observer moves towards a stationary source of sound. The percentage change in the apparent frequency is
AzeroB0.05C0.1D0.2A sound source is moving towards a stationary observer with 1/10 of the speed of sound. The ratio of apparent to real frequency is
A109B(109)2C(1110)2D1110
Speed of sound wave is v. If a reflector moves towards a stationary source emitting waves of frequency f with speed u, the wavelength of reflected waves will be
View Solution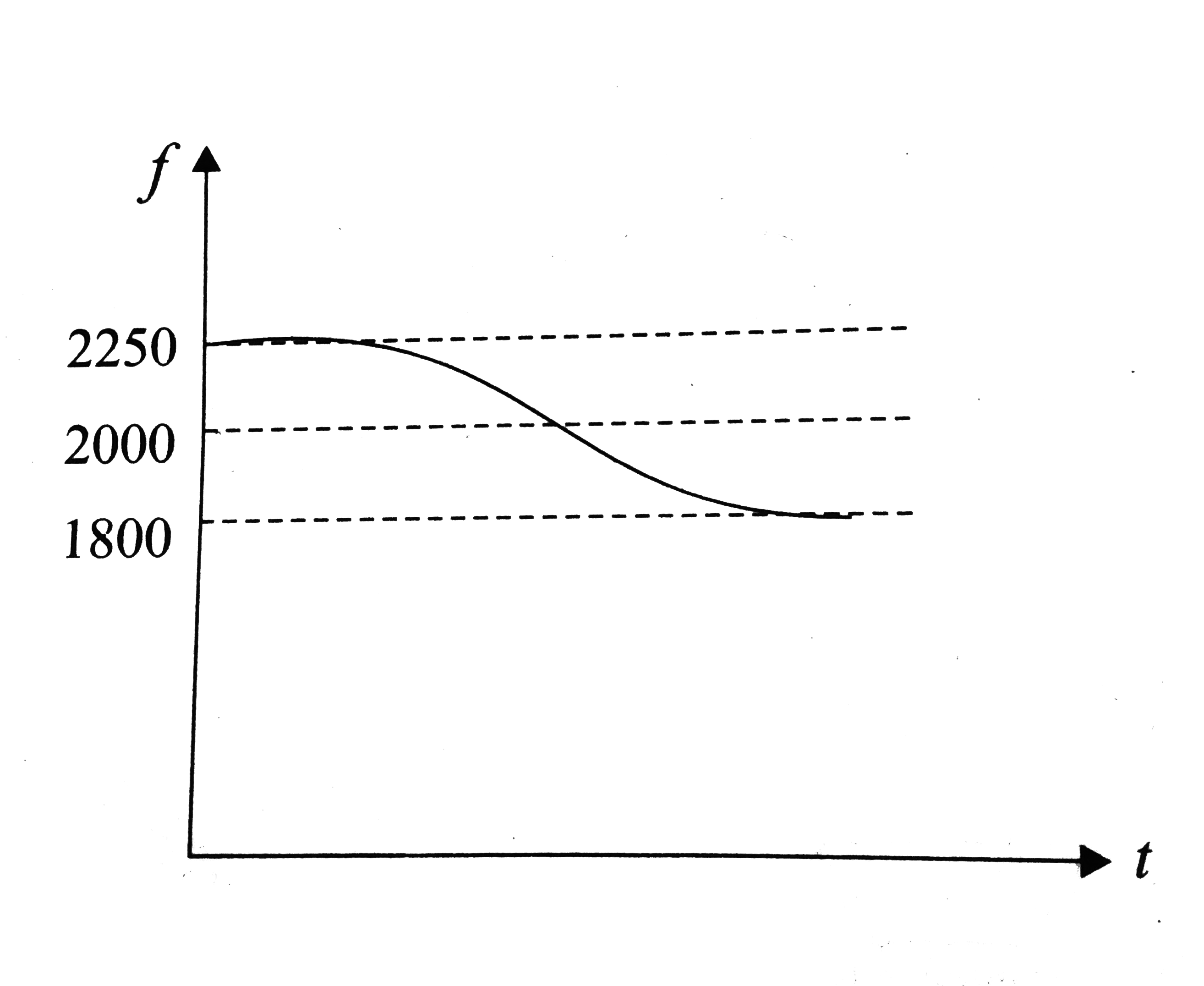
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300ms
View SolutionAn observer travelling with a constant velocity of 16.5ms−1, passes closes to a stationary source of sound and notices that there is a change of frequency of 50 Hz as he passes the source. Calculate the frequency of the source. (Speed of sound in air = 330 ms−1).
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionAn observer moves towards a stationary source of sound with a velocity one-fifth of the velocity of sound. What is the percentage increase in the apparent frequency?
View SolutionA sound source moves with a speed of 80m/s relative to still air toward a stationary listener. The frequency of sound is 200HZ and speed of sound in air is 340m/s. (a) Find the wavelength of the sound between the source and the listener. (b) Find the frequency heard by the listener.
View Solution
