A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening.
Let radius of semi-circle = r
∴ One side of rectangle = 2r and otherwise = x
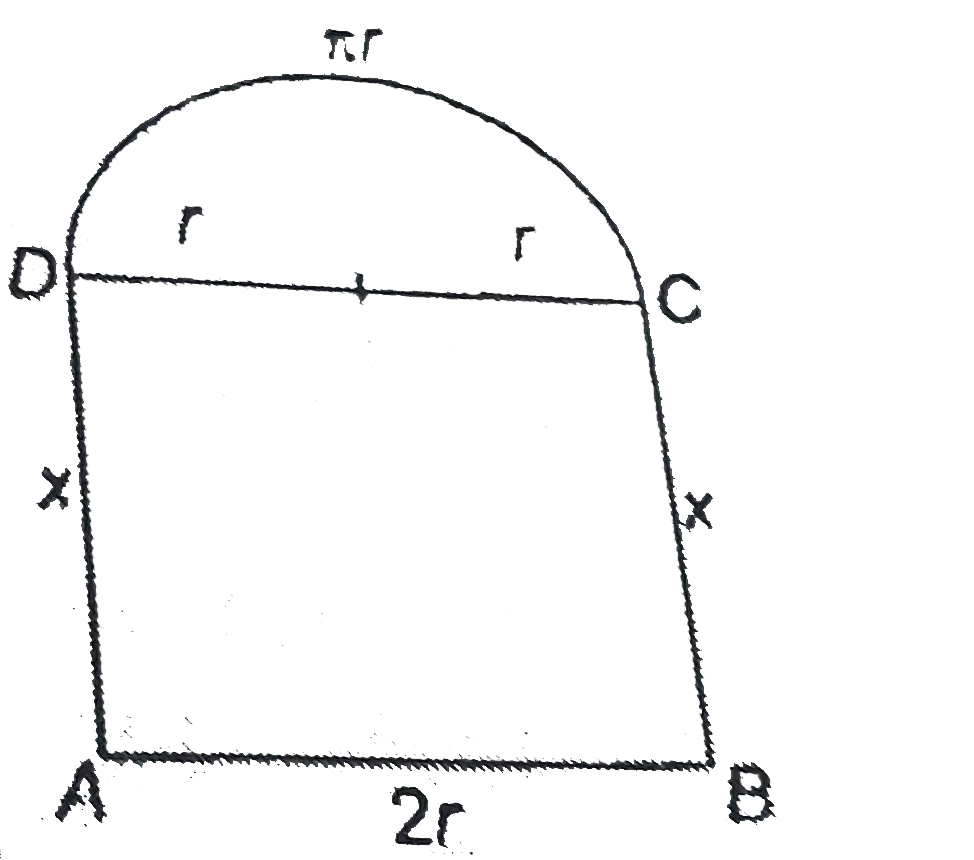
∴ P=perimeter = 10 (Given)
⇒2x+2r+12(2πr)=10
⇒2x=10−r(π+2) ….(1)
Again let A be the area of the window.
∴ A= area of semi - circle + area of rectangle = 12πr2+2rx
⇒A=12πr2+r[10−r(π+2)] [ From eqn. (1)]
12πr2+10r−r2π−2r2
=10r−πr22−2r2
⇒dAdr=10−πr−4r .....(2)
and d2Adr2=−π−4 ...(3)
For maxima/minima dAdr=0
⇒10−πr−4r=0⇒10=(4+π)r
⇒r=104+π
put r=104+π in equation (3) ,d2Adr2<0
∴ A has local maximum value at r=104+π
∴ radius of semicircle r=104+π ....(4)
and a side of rectangle = 2r=2×104+π=204+π
From equation (1) other side of rectangle x=12[10−r(π+2)]
12[10−(10π+4)(π+2)] [ From eqn. (4)
=10π+40−10π−202(π+4)
=202(π+4)=10π+4
∴ The light emitting from the window will be maximum when the area will be maximum, so the dimensions of the window are
radius =r=10π+4,length =2r=20π+4,breadth =x=10π+4.
Topper's Solved these Questions
Similar Questions
A window is in the form of a rectangle surmounted by a semi-circular opening. The total perimeter of the window is 10 meters. Find the dimensions of the rectangle so as to admit maximum light through the whole opening.
View SolutionA window is in the shape of a rectangle surmounted by a semi circle. If the perimeter of the window is of fixed length k then the maximum area of the window is
View SolutionA window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 m, find the dimensions of the rectangle that will produce the largest area of the window.
View SolutionA large window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 metres find the dimensions of the rectangle that will produce the largest area of the window.
View SolutionA window is in the form of a rectangle, together with a semi-circle on its top side as diameter. If the perimeter of the window is 80 inches, determine the dimensions of the rectangle, so that a maximum amount of light may be admitted.
View SolutionA window of perimeter P (including the base of the arch) is in the form of a rectangle surrounded by a semi-circle. The semi-circular portion is fitted with the colored glass while the rectangular part is fitted with the clear glass that transmits three times as much light per square meter as the colored glass does. What is the ratio for the sides of the rectangle so that the window transmits the maximum light?
View SolutionA ladder 10m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
View SolutionLength of a horizontal arm of ends of both the vertical arms pressure P0=105N/m2. A liquid of density ρ=103kg/m3 is poured in the tube such that liquid just fills the horizontal part of the tube as a shown in Fig. Now one end of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed ω0=√40/3rad/sec. If length of each vertical arm is a=1m and in the sealed end liquid rises to a height y=1/2m, find pressure in the sealed tube during rotation. (in ×105N/m2)

View SolutionA sheet of area 40m2 is used to make an open tank with square base. Find the dimensions of the base such that the volume of this tank is maximum.
View SolutionIn a double slit interference experiment, the separation between the slits is 1.0 mm, the wavelength of light used is 5.0x10−7 m and the distance of the screen from the slits is 1.0 m. (a) Find the distance of the centre of the first minimum from the centre of the central maximum. (b) How many bright fringes are formed in one centimeter width on the screen ?
View Solution
