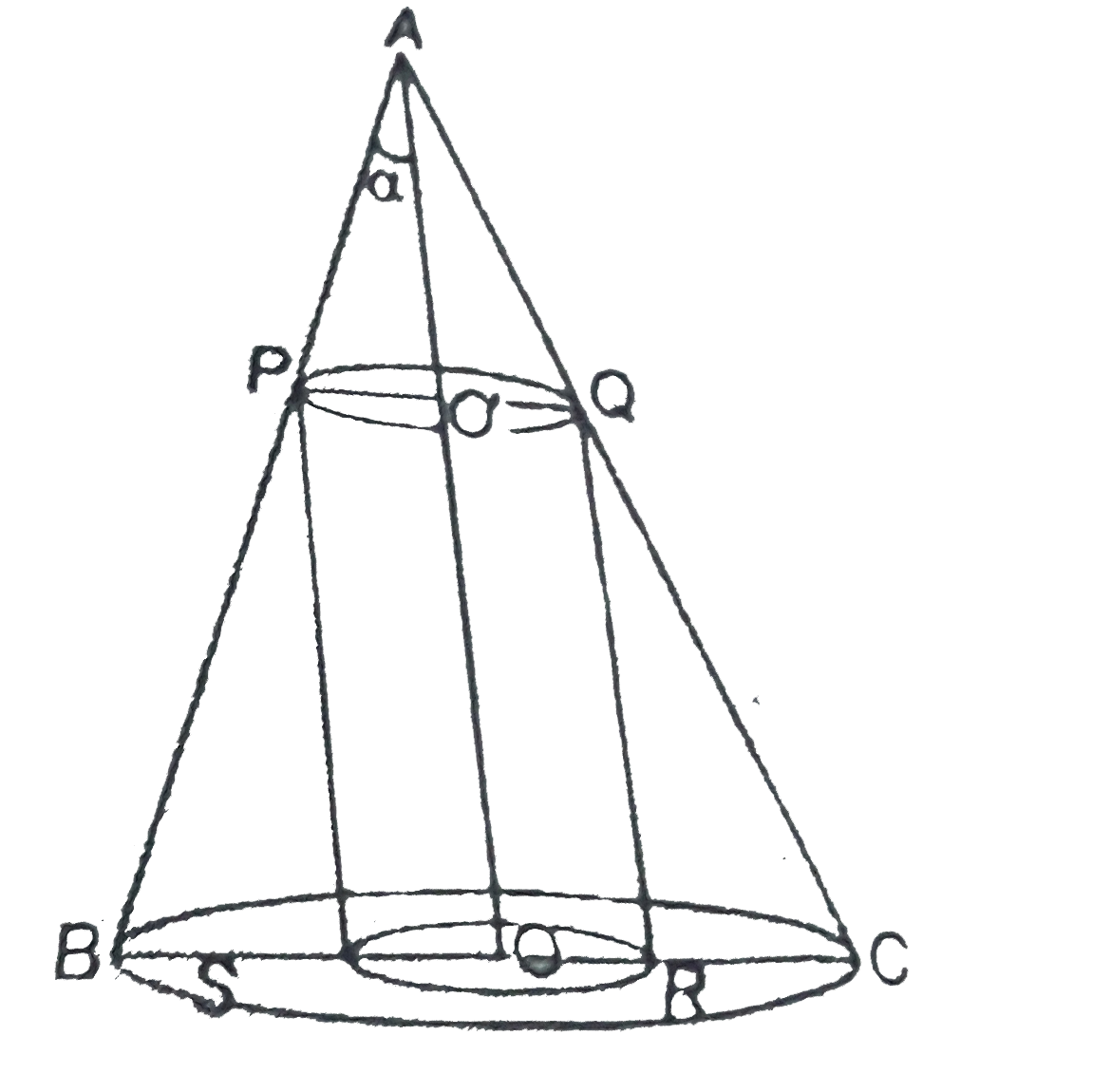
Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle is one-third that of the cone and the greatest volume of cylinder is $\frac{4}{27} π h^{3} {tan}^{2} α .$

Video Solution

Text Solution

Verified by Experts

Let height of cone AO = h and $∠ B A O = α$
Let radius of cylinder
O'P = x
In $Δ A P O', tan α = \frac{P O'}{A O'}$
$\Rightarrow A O' = x cot α$
$∴ O' O = A O - A O'$
$= h - x cot α$
Now, volume of cylinder
$V = π x^{2} \cdot (O O')$
$= π x^{2} (h - x cot α)$
$= π (h x^{2} - x^{3} cot α)$
$\Rightarrow \frac{d V}{d x} = π (2 h x - 3 x^{2} cot α)$
and $\frac{d^{2} V}{{d x}^{2}} = π (2 h - 6 x cot α)$
For maxima/minima, $\frac{d V}{d x} = 0$
$\Rightarrow 2 h x = 3 x^{2} cot α \Rightarrow x = \frac{2 h}{3} tan α$
at $x = \frac{2 h}{3} tan α$
$\frac{d^{2} V}{{d x}^{2}} = π (2 h - 4 h) = - 2 π h < 0$
$\Rightarrow$ Volume V is maximum.
Now, maximum volume
$V = π {h {(\frac{2 h}{3} tan α)}^{2} - {(\frac{2 h}{3} tan α)}^{3} cot α}$
$= π h^{3} {tan}^{2} α (\frac{4}{9} - \frac{8}{27}) = \frac{4}{27} π h^{3} {tan}^{2} α$ .

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF DERIVATIVES-Miscellaneous Exercise

Home
Ask Doubt
Profile