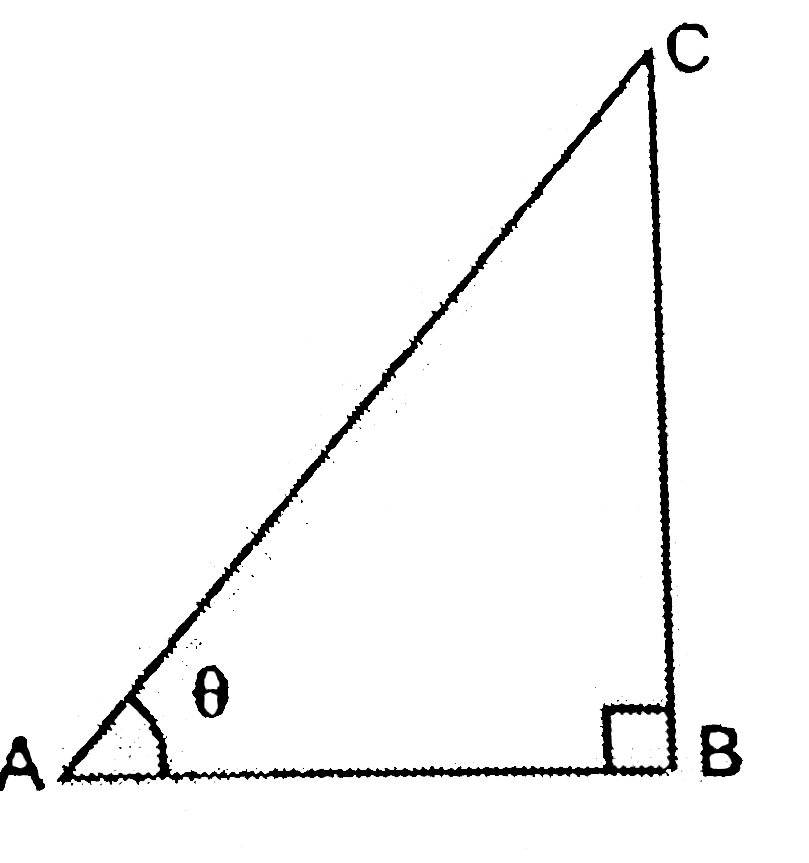
If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is $\frac{π}{3}$ .

Video Solution

Text Solution

Verified by Experts

Let, In $Δ A B C, ∠ B = 90^{\circ}$
Let AB = x and AC = y
Then x+y = k
Which is given a constant.
$B C = \sqrt{A C^{2} - A B^{2}}$
$= \sqrt{y^{2} - x^{2}}$
$= \sqrt{{(k - x)}^{2} - x^{2}}$
$= \sqrt{k^{2} - 2 k x}$
$Now area of Δ A B C$
$Δ = \frac{1}{2} \times A B \times B C$
$= \frac{1}{2} \times x \times \sqrt{k^{2} - 2 k x}$
$\Rightarrow Δ^{2} = \frac{1}{4} x^{2} (k^{2} - 2 k x)$
Let $Δ^{2} = S$ ,
$∴ S = \frac{1}{4} k (k x^{2} - 2 x^{3})$
$\Rightarrow \frac{d S}{d x} = \frac{1}{4} k (2 k x - 6 x^{2})$
For maxima/minima
$\frac{d S}{d x} = 0$
$\Rightarrow 2 k x - 6 x^{2} = 0$
$\Rightarrow x = \frac{k}{3}$
and $\frac{d^{2} S}{{d x}^{2}} = \frac{1}{4} k (2 k - 12 x)$
$at x = \frac{k}{3}$
$\frac{d^{2} S}{{d x}^{2}} = \frac{1}{4} k (2 k - 4 k) = - \frac{k^{2}}{2} < 0$
$∴ At x = \frac{k}{3}, \cdot$ S is maximum
$\Rightarrow At x = \frac{k}{3}, Δ^{2}$ is maximum
$\Rightarrow At x = \frac{k}{3}, Δ$ is maximum
and $y = k - \frac{k}{3} = \frac{2 k}{3}$
If $∠ B A C = θ,$ then
$\cos θ = \frac{A B}{A C} = \frac{x}{y} = \frac{k / 3}{2 k / 3} = \frac{1}{2}$
$\Rightarrow θ = π / 3$ for maximum area.

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

If the sum of two sides, other than hypotenuse of a right-angled triangle is 17cm and the perimeter is 30cm, then the lengths of two sides are:
A7cm, 10cm
B4cm, 13cm
C5cm, 12cm
D6cm, 11cm

NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF DERIVATIVES-Miscellaneous Exercise

Home
Ask Doubt
Profile