In trapezium ABCD. AB||DC and DC = 2AB. A line segment EF drawn parallel to AB cuts AD in F and BC in E such that BEEC=34 .
Diagonal DB intersects EF at G. prove that &EF= 10AB.
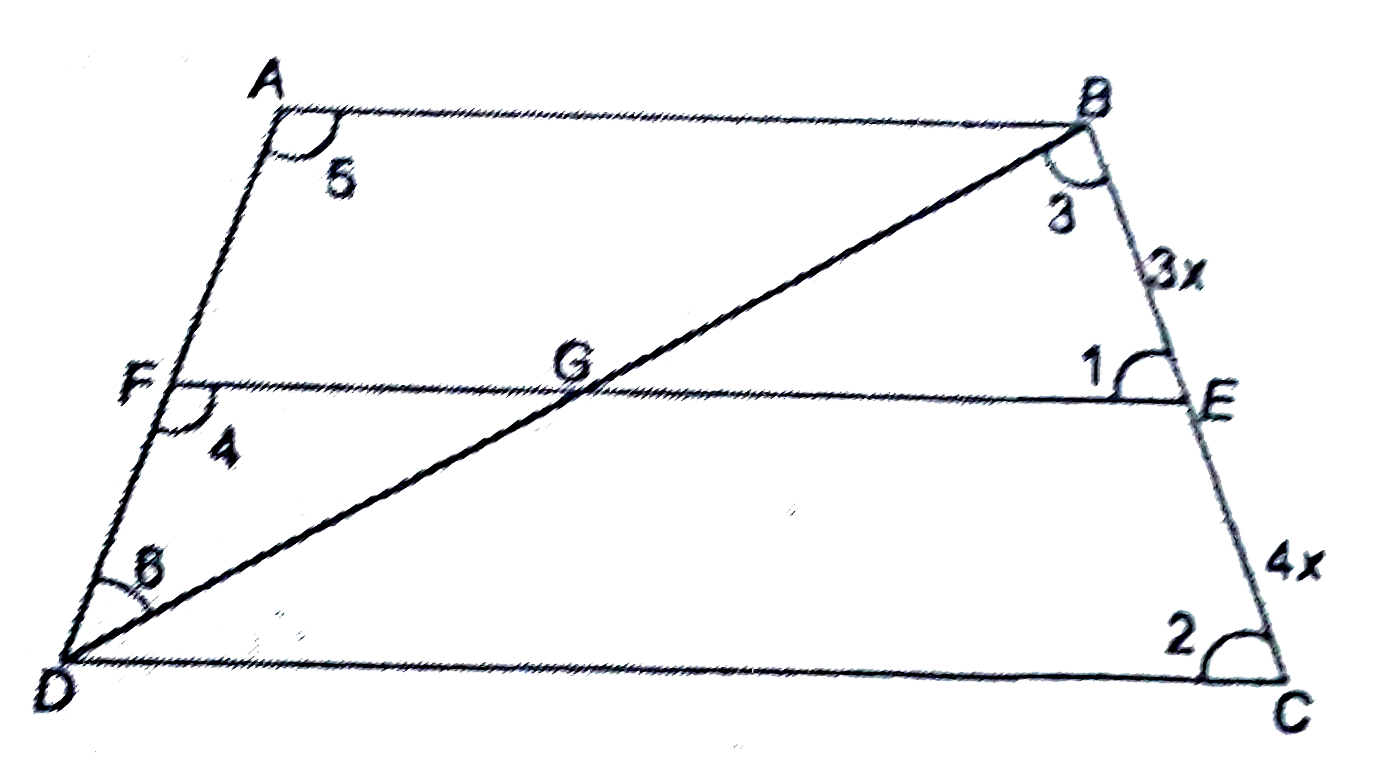
Since GE||DC
BEEC=BGGD (by B.P theorem ) …(1)
Also GF||AB
AFFD=BGGD (by B.P theorem) ….(2)
from (1) and (2) , we get
AFFD=BEEC=34
In △BGEand△BDC
∠1=∠2 (corresponding ∠s as GE||DC)
∠3=∠3 (common)
△BGE~△BDC (AA corocllary)
GEDC=BEBC (corresponding sides of similar triangles are proportional)
GE2AB=37(DC=2AB)
⇒GEAB=67 ....(4)
Now in △DFGand△DAB
∠4=∠5 ( corresponding ∠s as FG||AB)
∠6=∠6 (common)
△DFG~△DAB (AA corollary)
FGAB=DFDA
⇒FGAB47 ( from 3)...(5))
Adding (4) and (5) , we get
GEAB+GFAB=67+47
GE+GFAB=107
EFAB=107
⇒7EF=10AB Hence proved.
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Problems From NCERT/ Exemplar
Explore 14 Videos
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Exercise 6a
Explore 24 Videos
- STATISTICS Book:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHAN ENGLISHChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
In trapezium ABCD, AB/DC and DC=2 AB. EF, drawn parallel to AB cuts AD in F and BC in E such that 4BE= 3 EC. Diagonal DB intersects FE at point G. Prove that: 7EF= 10AB
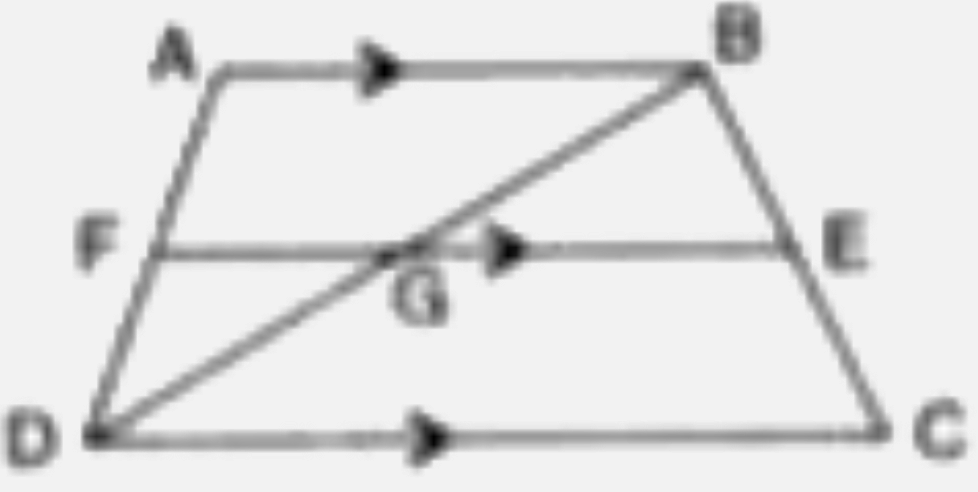
View SolutionIn a trapezium ABCD, AB/DC, E is mid-point of aD. A line through E and parallel to AB intersects BC at point F. Show that:
2EF=AB+DC
View SolutionDraw a line segment EF equal to a given line segment AB
View SolutionA line segment DE is drawn parallel to base BC of A ABC which cuts AB at point D and AC at point E. If AB = 5 BD and EC = 3.2 cm, find the length of AE.
View SolutionABCD is a trapezium with AB∣∣DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
View SolutionO is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB||DC. Through O , aline segment PQ is drawn parallel to AB meeting AD in P and BC in Q, prove that PO=QO.
View SolutionE is the mid-point of the side AD of the tarapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. Show that F is the mid-points of BC.
View SolutionIn trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠A=60∘. Find:
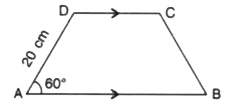
(i) length of AB
View SolutionIn trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that : AB + DC = 2EF.
View SolutionIn quadrilateral ABCD, AB=DC and AD=BC. Prove that the sides AB and DC are parallel to each other.
View Solution

