A line segment DE is drawn parallel to base BC of A ABC which cuts AB at point D and AC at point E. If AB = 5 BD and EC = 3.2 cm, find the length of AE.
The correct Answer is:12.8cm
To solve the problem step by step, we will use the properties of similar triangles.
Step 1: Understand the relationship between segments
Given that AB=5×BD, we can express AD in terms of BD:
AD=AB−BD=5BD−BD=4BD
Step 2: Set up the ratio of segments
Now we can set up the ratio of the segments AD and AB:
ADAB=4BD5BD=45
Step 3: Use the property of similar triangles
Since DE is parallel to BC, triangles ADE and ABC are similar by the AA (Angle-Angle) similarity criterion. Therefore, the ratios of corresponding sides are equal:
ADAB=AEAC
Step 4: Express AC in terms of AE
We know that AC=AE+EC. Given EC=3.2 cm, we can substitute this into our ratio:
ADAB=AEAE+3.2
Step 5: Substitute the known values into the ratio
Now, substituting the known values into the equation:
45=AEAE+3.2
Step 6: Cross-multiply to solve for AE
Cross-multiplying gives:
4(AE+3.2)=5AE
Expanding this:
4AE+12.8=5AE
Step 7: Rearranging the equation
Rearranging the equation to isolate AE:
12.8=5AE−4AE
12.8=AE
Step 8: Conclusion
Thus, the length of AE is:
AE=12.8cm
---
Given that AB=5×BD, we can express AD in terms of BD:
AD=AB−BD=5BD−BD=4BD
Now we can set up the ratio of the segments AD and AB:
ADAB=4BD5BD=45
Since DE is parallel to BC, triangles ADE and ABC are similar by the AA (Angle-Angle) similarity criterion. Therefore, the ratios of corresponding sides are equal:
ADAB=AEAC
We know that AC=AE+EC. Given EC=3.2 cm, we can substitute this into our ratio:
ADAB=AEAE+3.2
Now, substituting the known values into the equation:
45=AEAE+3.2
Cross-multiplying gives:
4(AE+3.2)=5AE
Expanding this:
4AE+12.8=5AE
Rearranging the equation to isolate AE:
12.8=5AE−4AE
12.8=AE
Thus, the length of AE is:
AE=12.8cm
Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(C)
24 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(D)
18 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(A)
48 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)BOOK - ICSECHAPTER - SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)EXERCISE - Exercise 6(e )
18 Videos
Similar Questions
Knowledge Check
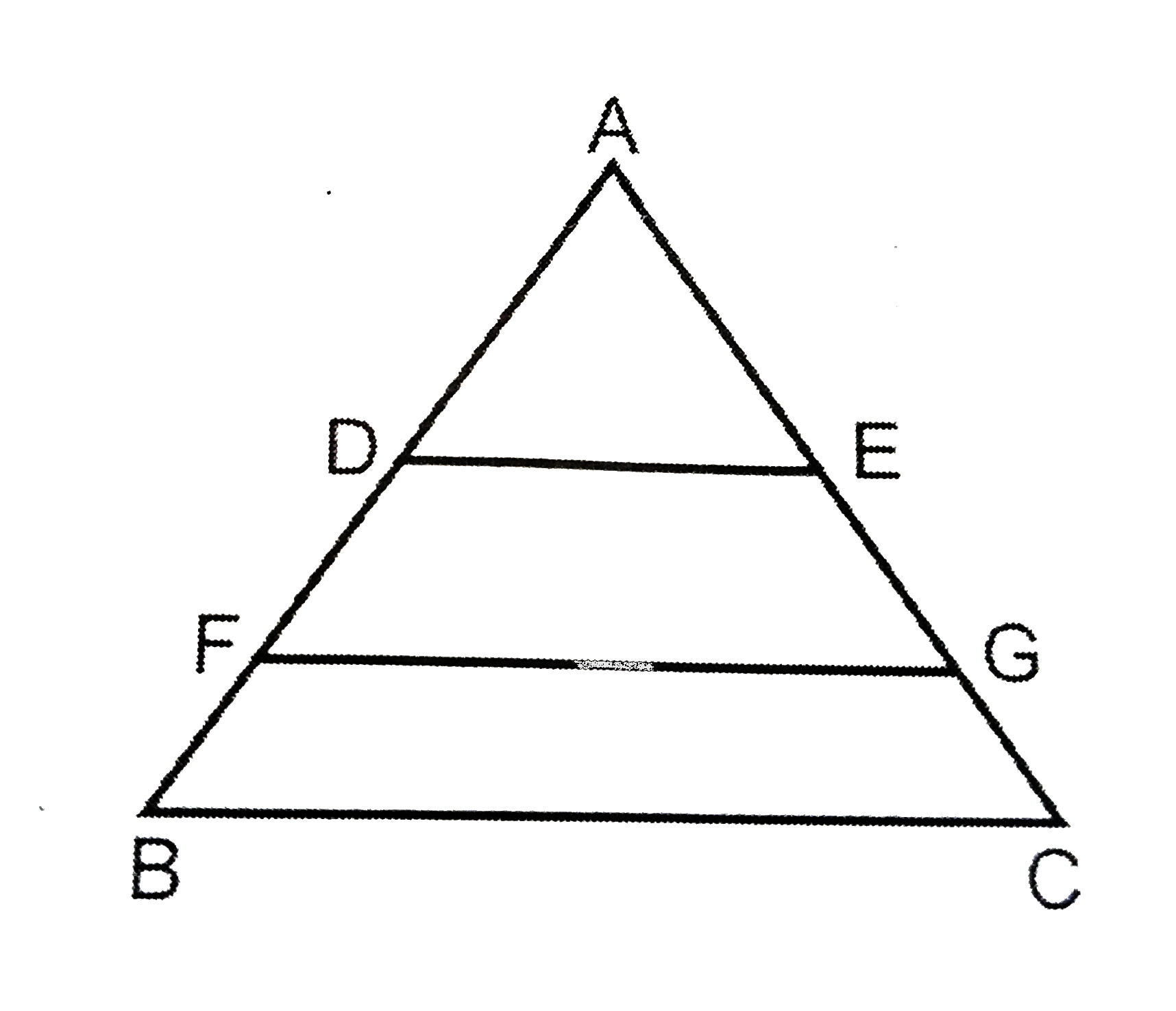
In ΔABC,D and E are the mid-points of AB and AC. Again, F and G are the mid-points of DB and EC, If BC=12,what is the length of FG?A4B6C8D9
In the figure, EF || AC, BC = 10 cm, AB = 13 cm and EC = 2 cm, find AF
View SolutionIn triangle ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm, find the perimeter of the parallelogram BDEF.
View SolutionIn the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB= 12 cm, BC= 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
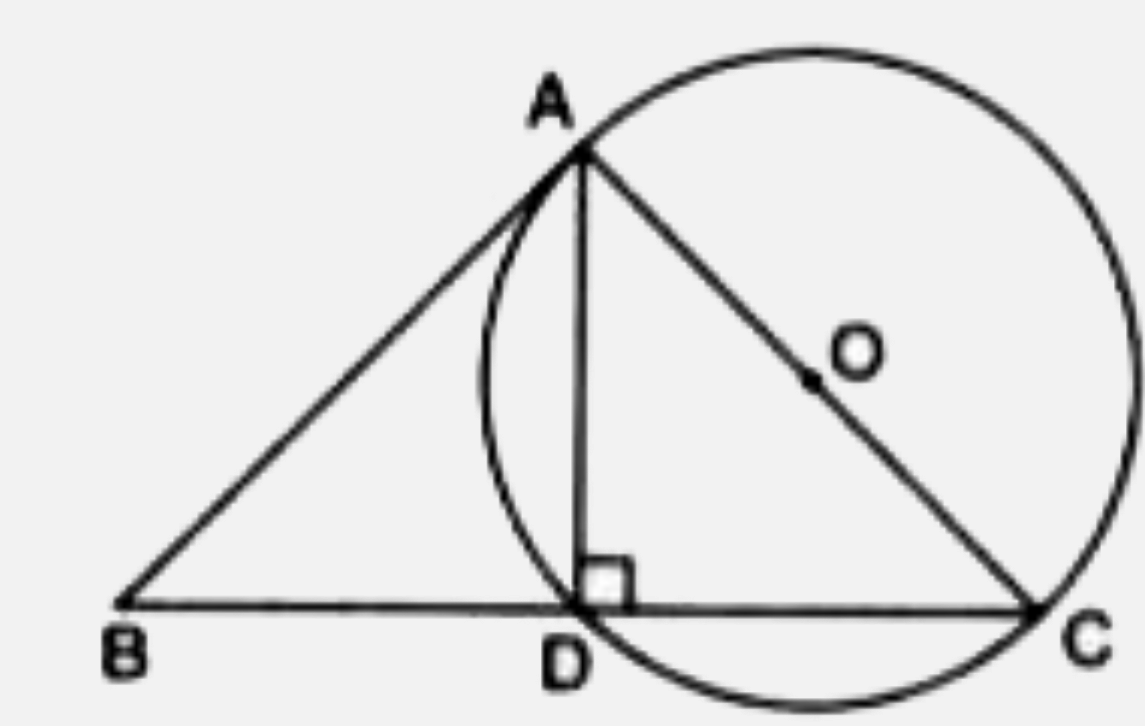
View SolutionThe angle A of the triangle ABC is a right angle. The circle on AC as diameter cuts BC at point D. If BD=9cm and DC = 7 cm, calculate the length of AB.
View SolutionIf lines AB,AC,AD and AE are parallel to a line l show that points A,B,C,D and E are collinear.
View SolutionIn the following figure, point D divides AB in the ratio 3: 5. Find :

Also if :
BC = 4.8 cm, find the length of DE.
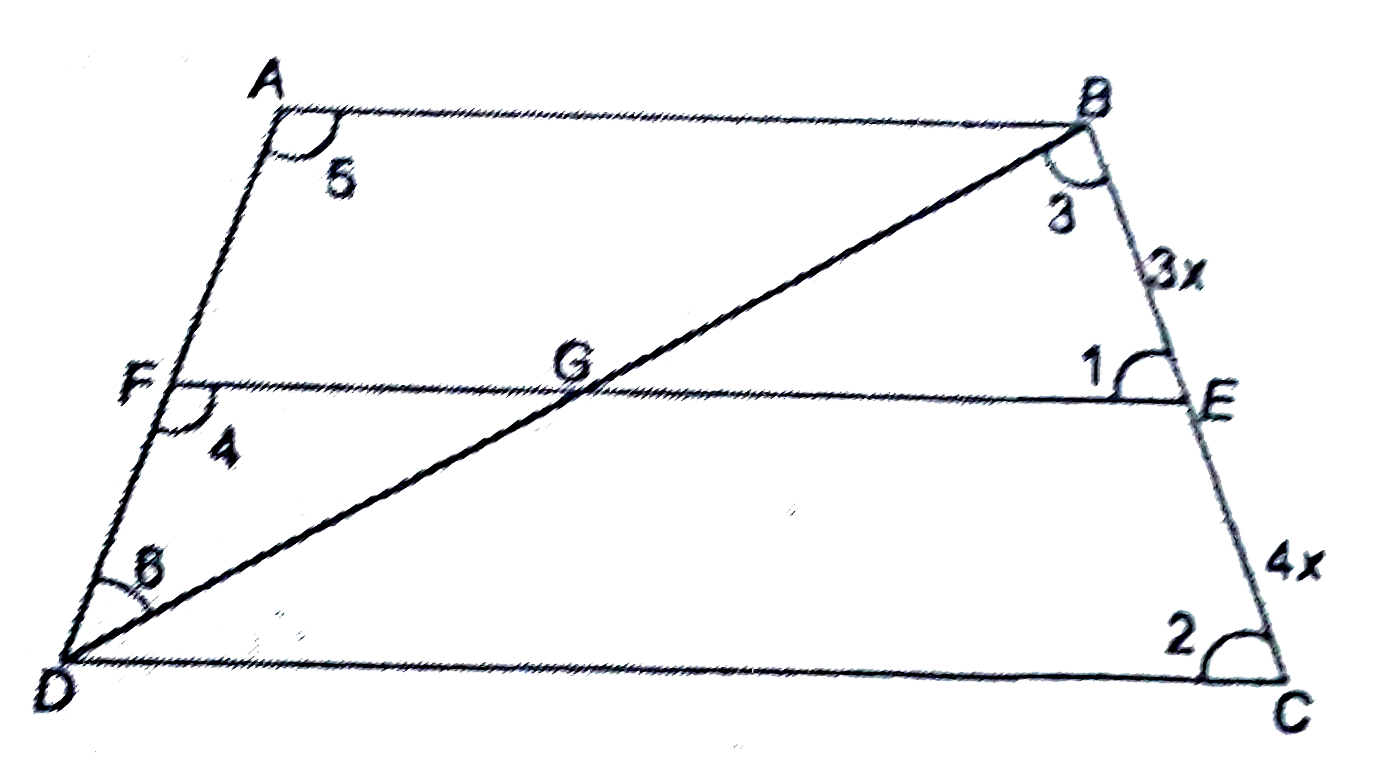
View SolutionIn trapezium ABCD. AB||DC and DC = 2AB. A line segment EF drawn parallel to AB cuts AD in F and BC in E such that BEEC=34 .
Diagonal DB intersects EF at G. prove that &EF= 10AB.
View Solution
