If lines AB,AC,AD and AE are parallel to a line l show that points A,B,C,D and E are collinear.
To show that points A, B, C, D, and E are collinear given that lines AB, AC, AD, and AE are all parallel to a line l, we can follow these steps:
1. Understanding Collinearity:
- Collinear points are points that lie on the same straight line.
2. Identify the Given Information:
- We have lines AB, AC, AD, and AE that are all parallel to line l.
3. Draw Line l:
- Start by drawing line l on a piece of paper. This will serve as our reference line.
4. Draw Parallel Lines:
- From point A, draw lines AB, AC, AD, and AE such that each of these lines is parallel to line l.
- Since all these lines are drawn from the same point A and are parallel to line l, they will never intersect line l.
5. Extend the Parallel Lines:
- Extend lines AB, AC, AD, and AE in both directions.
- Since they are parallel to line l, they will maintain the same direction as line l.
6. Conclusion on Collinearity:
- Since all lines (AB, AC, AD, and AE) are parallel to line l and originate from point A, the points B, C, D, and E must lie on the same straight line that is parallel to line l.
- Therefore, points A, B, C, D, and E are collinear.
Final Statement:
Thus, we have shown that points A, B, C, D, and E are collinear because they all lie on lines that are parallel to line l.
- Collinear points are points that lie on the same straight line.
- We have lines AB, AC, AD, and AE that are all parallel to line l.
- Start by drawing line l on a piece of paper. This will serve as our reference line.
- From point A, draw lines AB, AC, AD, and AE such that each of these lines is parallel to line l.
- Since all these lines are drawn from the same point A and are parallel to line l, they will never intersect line l.
- Extend lines AB, AC, AD, and AE in both directions.
- Since they are parallel to line l, they will maintain the same direction as line l.
- Since all lines (AB, AC, AD, and AE) are parallel to line l and originate from point A, the points B, C, D, and E must lie on the same straight line that is parallel to line l.
- Therefore, points A, B, C, D, and E are collinear.
Thus, we have shown that points A, B, C, D, and E are collinear because they all lie on lines that are parallel to line l.
Topper's Solved these Questions
- INTRODUCTION TO EUCLID'S GEOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:INTRODUCTION TO EUCLID'S GEOMETRYExercise:Problems From NCERT/exemplar
Explore 4 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:INTRODUCTION TO EUCLID'S GEOMETRYExercise:Exercise
Explore 8 Videos
- HERONS'S FORMULABook:NAGEEN PRAKASHAN ENGLISHChapter:HERONS'S FORMULAExercise:Revision Exercise
Explore 11 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Revision Exercise
Explore 12 Videos
Similar Questions
Find the equation of the line through the points A(-1, 3) and B(0, 2). Hence, show that the points A, B and C(1, 1) are collinear.
View SolutionIn Figure, ABC is a triangle in which AB=AC. Point DandE are points on the sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View Solution
Knowledge Check
A, B,C and D are points on a line such that point B biscets line AC and point A bisects line CD. What is the ratio of AB to CD ?
A1/4B1/3C1/2D2/3If A, B, C, D and E are points in a plane such that line CD bisects ∠ACB and line CB bisects right angle ∠ACE, then ∠DCE =
A22.5∘B45∘C575∘D67.5∘
In the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
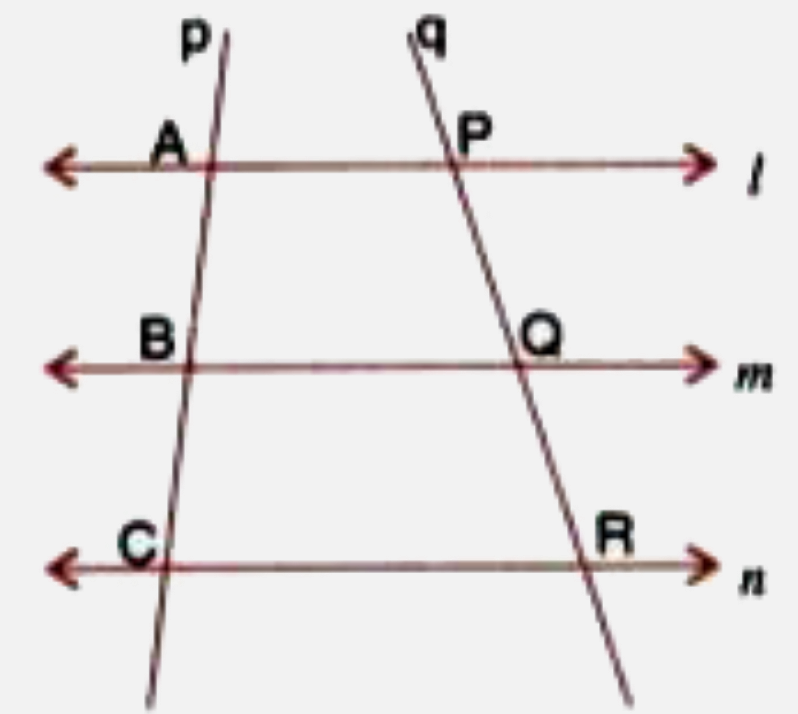
Prove that : ABBC=PQQR
Join A and R. Let AR meets BQ at point D.
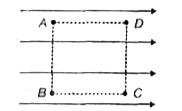
View SolutionFigure shows four points A, B, C and D in uniform electric field →E. The line AB and CD are perpendicular and BC and AD are parallel to the field lines. If VA,VB,VCandVD are electric potential at A, B,C,D choose the correct option.
View SolutionTwo circle intersect in A and B and AC and AD are respectively the diameters of the circles. Prove that C,B,D are collinear.
View SolutionA line segment DE is drawn parallel to base BC of A ABC which cuts AB at point D and AC at point E. If AB = 5 BD and EC = 3.2 cm, find the length of AE.
View SolutionIn the adjoining figure
(a) Name
(i) Parallel lines
(ii) all pairs of intersecting lines.
(iii) concurrent lines.
( b) State whether true of false.
(i) points A,B and D are collinear.
(ii) lines AB and ED intersects at C .
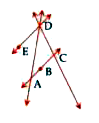
View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD and FE bisect each other.
View Solution

