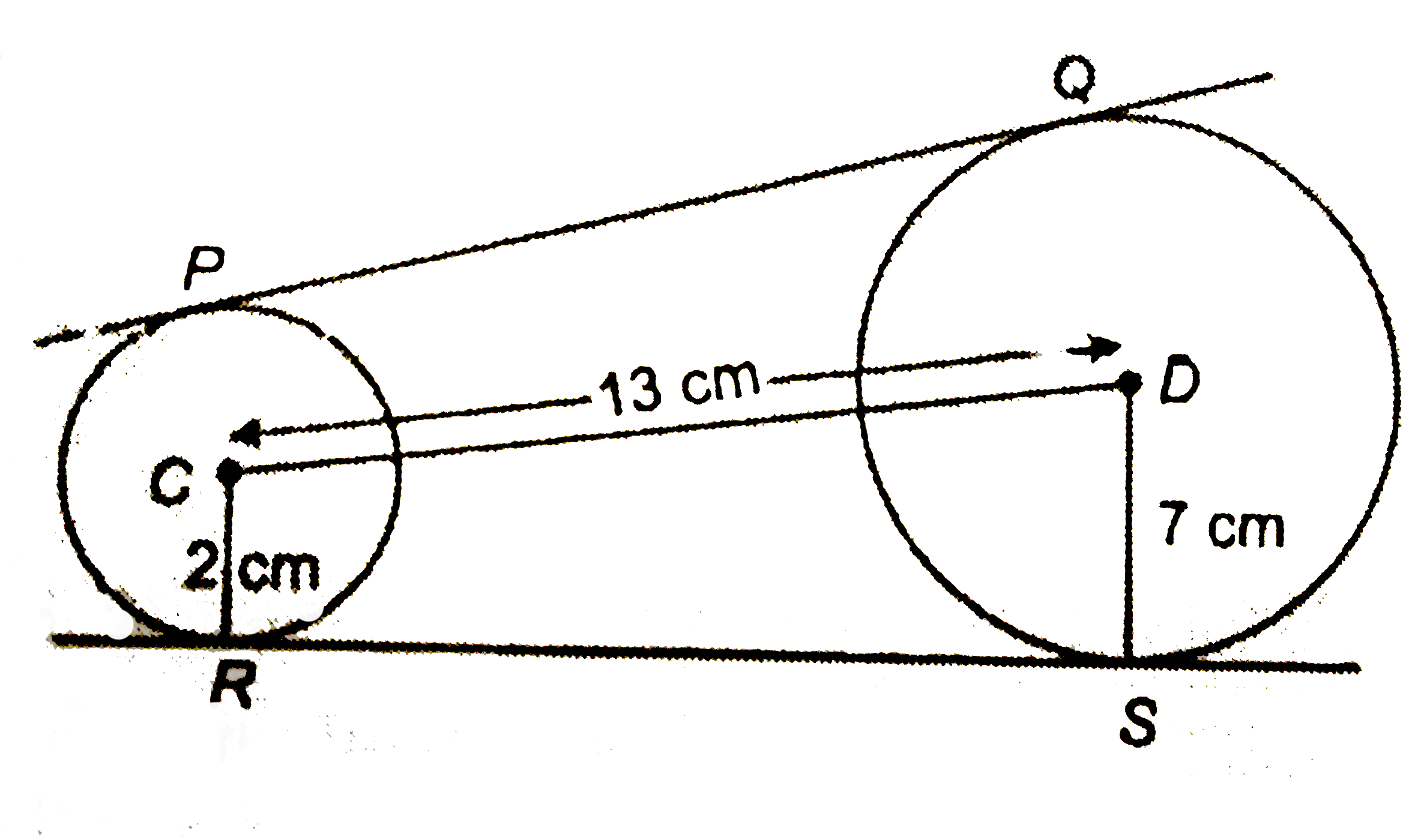
In the given diagram, PQ and RS are common tangents to the two circles with centres C and D. Find the length of PQ and hence area of trapexium RSDC.
54cm2
64cm2
50cm2
None
The correct Answer is:A
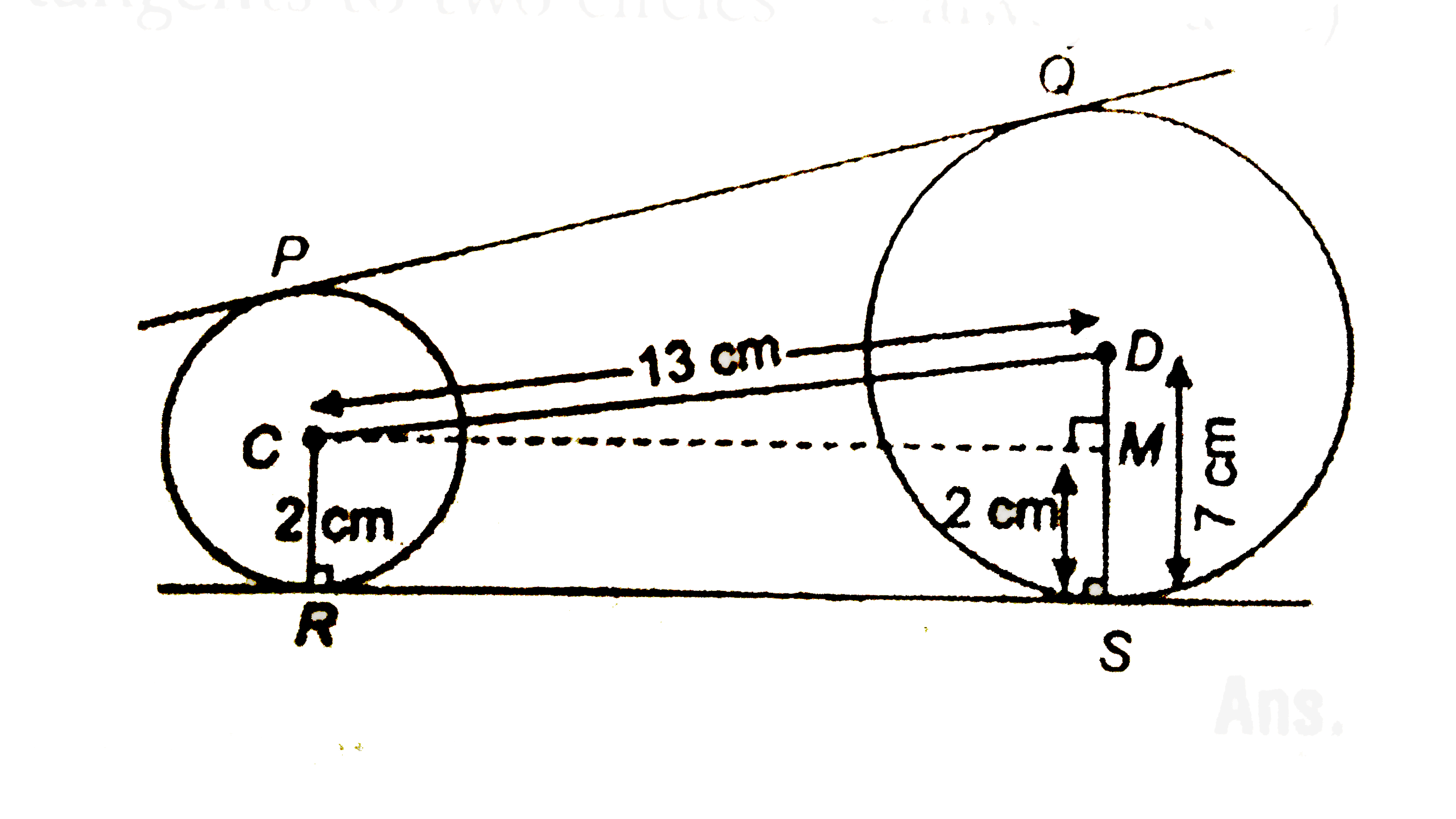
Draw CM||RS so that □CMSRbecomes a rectangle, Now, we have CR=2 cm, DS=7 cm and CD=13 cm
∴ DM=DS−MS
=DS−CR
=7−2=5cm
In right ΔDMC, by Pythagoras theorem,
CM2=CD2−DM2
=(13)2−(5)2=(12)2
∴ CM=12cm
⇒ RS=12cm (∵opposite sides of rectangle are equal)
∴ PQ=12cm (∵length of common tangents to two circles are always same)
=12×h(sum of parallel sides)
=12×CM(CR+DS)
=12×12(2+7)=54cm2
Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar
11 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise
32 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
10 Videos
Similar Questions
In the given figure, PT is a tangent to the circle with centre O. If OT=6cm and OP=10cm, thcn find the length of tangent PT.
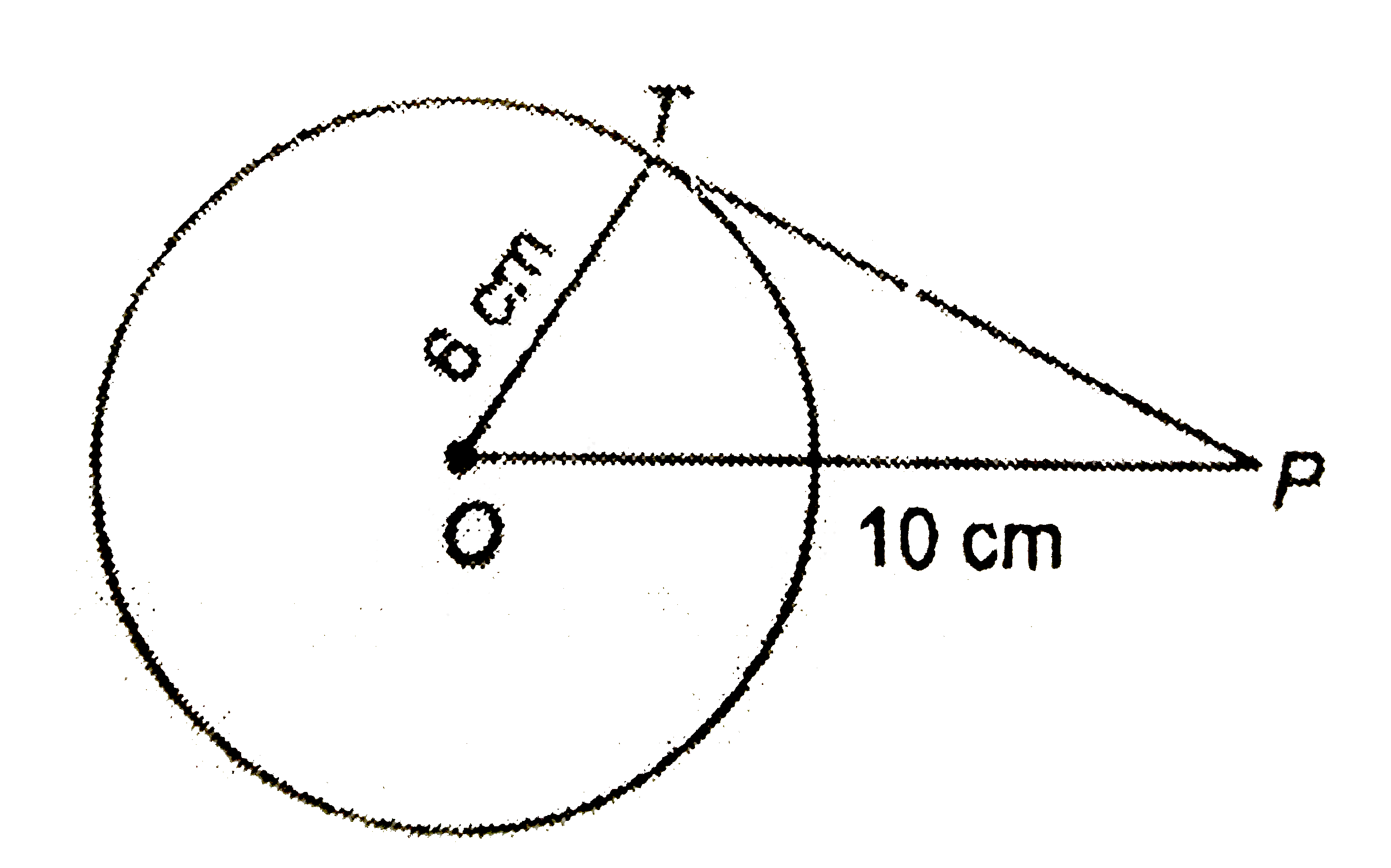
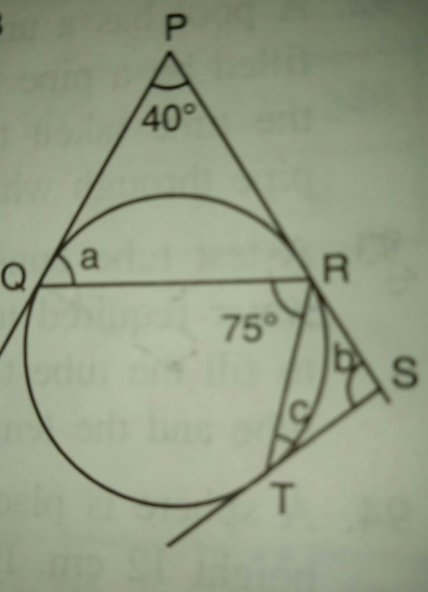
View SolutionIn the given figure, PQ, PR and ST are tangents to the same circle. If ∠P=40∘and∠QRT=75∘, find a, b and c
<
View SolutionIn the figure given below, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively.
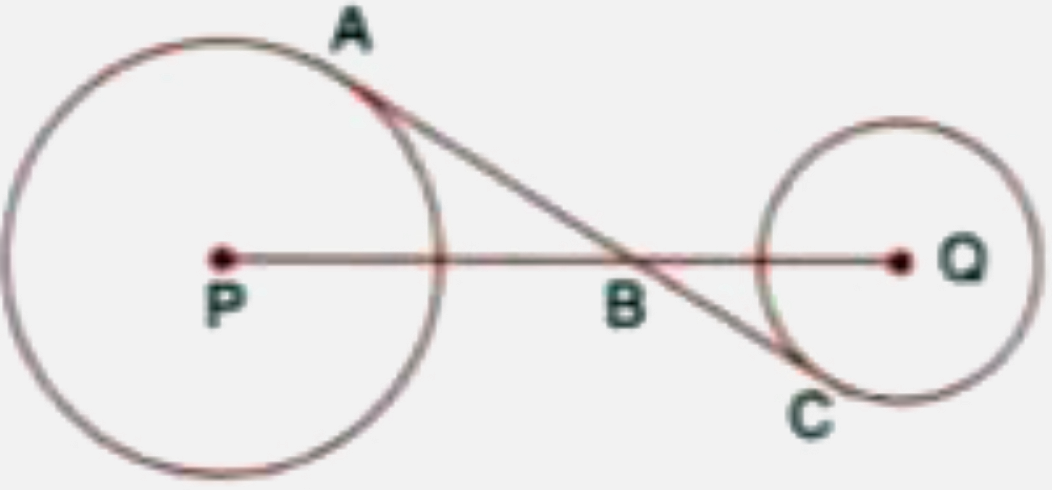
Given that AB=8 cm calculate PQ.
View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View Solution
In the figure shown above, ∠Q measures 70∘ , ¯¯¯¯¯¯PQ≅¯¯¯¯¯¯PR , and ¯¯¯¯¯¯PQ and ¯¯¯¯¯¯PR are tangent to the circle with center O at points A and B . Find , in degrees , the measure of ∠AOB.
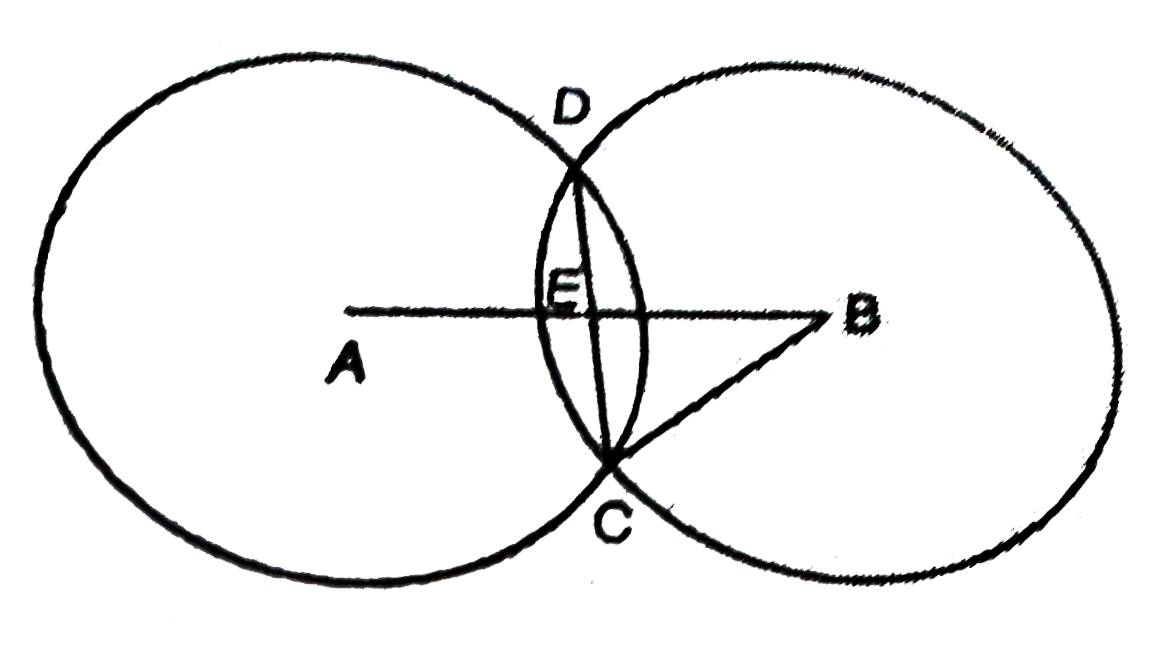
View SolutionIn the adjoining figure, A and B are the centres of two circles. If CB=17cm, EB=15cm, then find the length of common chord.
View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre C from an external point P, Prove that ∠QPR=2∠OQR.
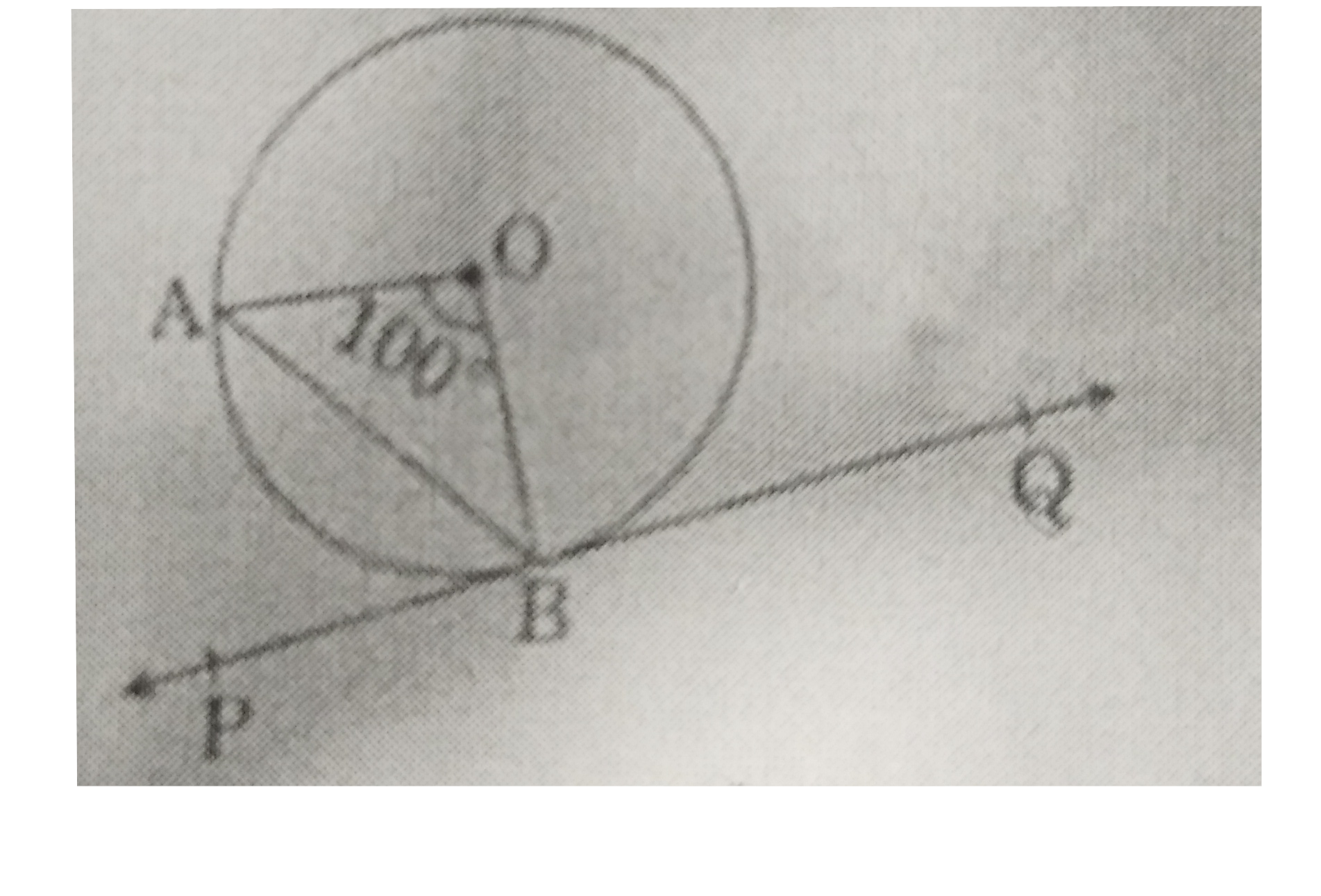
View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
View SolutionIn the figure, PO⊥QO. The tangents to the circle with centre O at P and Q intersect at a point T. Prove that PQ and OT are right bisectors of each other.

View SolutionTwo tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is cyclic quadrilateral.
View Solution
