On a square handkerchief, nine circular designs each of radius 7 cm are made (see Fig. 12.29). Find the area of the remaining portion of the handkerchief.
To find the area of the remaining portion of the handkerchief after making nine circular designs, we can follow these steps:
Step 1: Calculate the area of the square handkerchief.
Let the side length of the square handkerchief be s. Since there are nine circles arranged in a square formation, we can assume that the circles are arranged in a 3 by 3 grid. The diameter of each circle is 2×7cm=14cm.
Thus, the side length of the square handkerchief can be calculated as:
s=3×diameter of one circle=3×14cm=42cm
Now, we can calculate the area of the square:
Area of the square=s2=42cm×42cm=1764cm2
Step 2: Calculate the area of one circular design.
The area of one circle is given by the formula:
Area of one circle=πr2
Substituting the radius r=7cm:
Area of one circle=π×(7cm)2=π×49cm2
Using π≈227:
Area of one circle=227×49cm2=154cm2
Step 3: Calculate the total area of nine circular designs.
Since there are nine circles, the total area of the circular designs is:
Total area of circles=9×Area of one circle=9×154cm2=1386cm2
Step 4: Calculate the area of the remaining portion of the handkerchief.
To find the area of the remaining portion of the handkerchief, we subtract the total area of the circular designs from the area of the square handkerchief:
Area of remaining portion=Area of square−Total area of circles=1764cm2−1386cm2=378cm2
Final Answer:
The area of the remaining portion of the handkerchief is 378cm2.
---
Let the side length of the square handkerchief be s. Since there are nine circles arranged in a square formation, we can assume that the circles are arranged in a 3 by 3 grid. The diameter of each circle is 2×7cm=14cm.
s=3×diameter of one circle=3×14cm=42cm
Area of the square=s2=42cm×42cm=1764cm2
The area of one circle is given by the formula:
Area of one circle=πr2
Substituting the radius r=7cm:
Area of one circle=π×(7cm)2=π×49cm2
Using π≈227:
Area of one circle=227×49cm2=154cm2
Since there are nine circles, the total area of the circular designs is:
Total area of circles=9×Area of one circle=9×154cm2=1386cm2
To find the area of the remaining portion of the handkerchief, we subtract the total area of the circular designs from the area of the square handkerchief:
Area of remaining portion=Area of square−Total area of circles=1764cm2−1386cm2=378cm2
The area of the remaining portion of the handkerchief is 378cm2.
Topper's Solved these Questions
- AREA RELATED TO CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA RELATED TO CIRCLESExercise:Exercise 12 A
Explore 24 Videos
- AREA RELATED TO CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA RELATED TO CIRCLESExercise:Exercise 12 B
Explore 32 Videos
- AREA RELATED TO CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA RELATED TO CIRCLESExercise:Revision Exercise Long Answer Question
Explore 5 Videos
- ARITHMETIC PROGRESSIONBook:NAGEEN PRAKASHAN ENGLISHChapter:ARITHMETIC PROGRESSIONExercise:Revision Exercise Long Answer Question
Explore 5 Videos
Similar Questions
On a square handkerchief, nine circular designs each of radius 7 cm are made (see Figure). Find the area of the remaining portion of the handkerchief.
View SolutionFrom each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square.
View SolutionFrom each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square.
View SolutionFrom a rectangular cardboard sheet 145 cm long and 32 cm broad ,42 circular plates each of diameter 8 cm have been cut out . Find the area of the remaining portion of the sheet.
View SolutionA square park has each side of 100 m. At each corner of the park, there is a flower bed in the form of a quadrant of radius 14 m as shown in Fig. 15.37. Find the area of the remaining part of the park (Use π=22/7) . (FIGURE)
View SolutionA square is inscribed in a circle of radius 7 cm. Find the area of the square.
View SolutionIn Fig. 19, the radius of quarter circular plot taken is 2 m and radius of the flower bed is 2 m. Find the area of the remaining field.
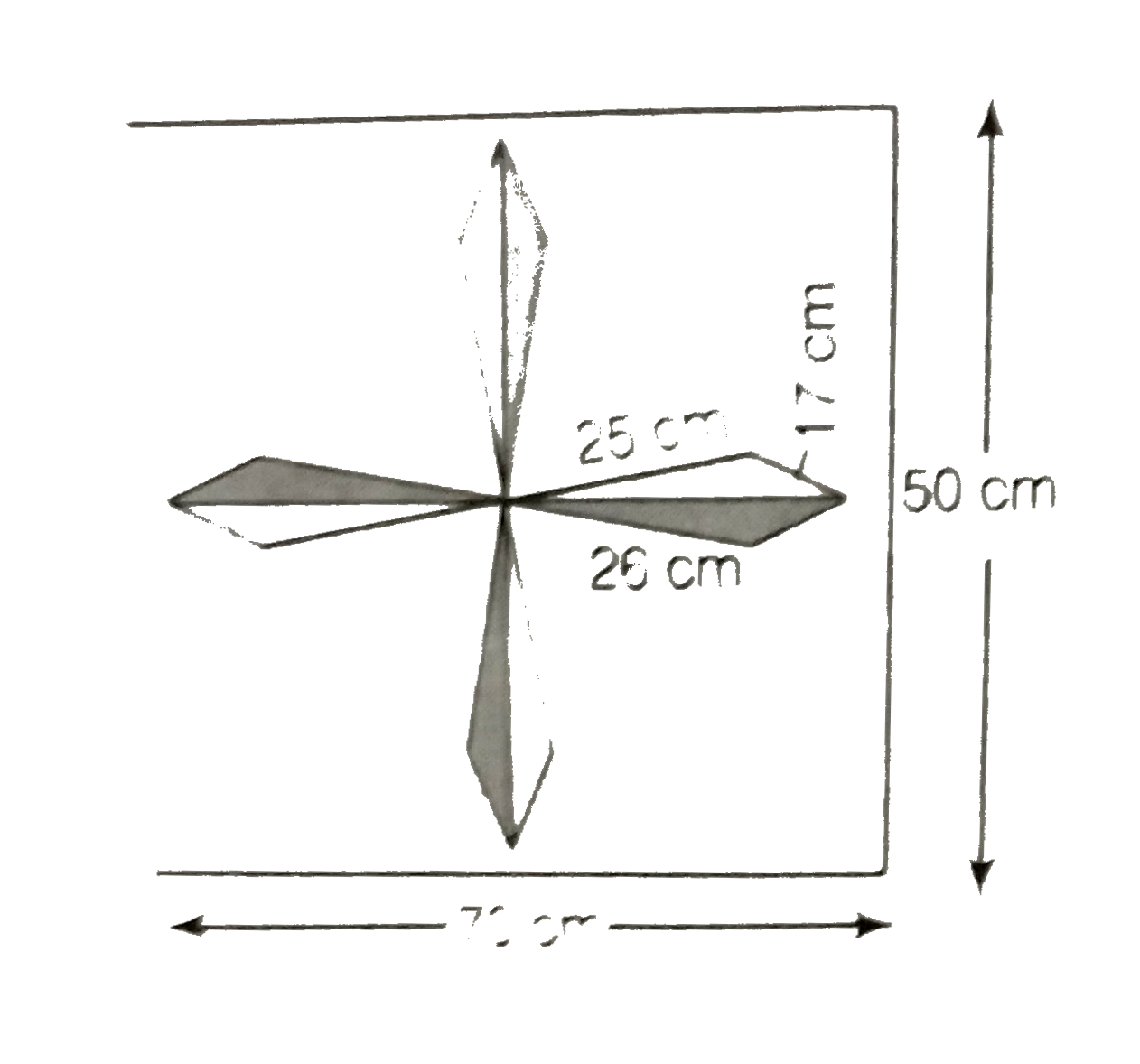
View SolutionA design is made on a rectangular tile of dimensions 50 cm×70 cm as shown in figure. The design shows 8 triangle, each of sides 26 cm, 17 cm and 25 cm. Find the total area of the design and the remaining area of the tiles.
View SolutionFrom a circular piece of cardboard of radius 3 cm two sectors of 90∘ have been cut off. Find the perimeter of the remaining portion nearest hundredth centimeters (Take π=227).
View SolutionFind the surface area of a sphere of radius 7 cm.
View Solution