In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the sides of the square where O and O are centres of the circles. Find the area of shaded region
Side of square = 28 cm
and radiu of each circle = 14 cm
Required area = area of square excluding the two sectors + area of two circles

Topper's Solved these Questions
- AREA RELATED TO CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA RELATED TO CIRCLESExercise:Exercise 12 A
Explore 24 Videos
- AREA RELATED TO CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA RELATED TO CIRCLESExercise:Exercise 12 B
Explore 32 Videos
- AREA RELATED TO CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA RELATED TO CIRCLESExercise:Revision Exercise Long Answer Question
Explore 5 Videos
- ARITHMETIC PROGRESSIONBook:NAGEEN PRAKASHAN ENGLISHChapter:ARITHMETIC PROGRESSIONExercise:Revision Exercise Long Answer Question
Explore 5 Videos
Similar Questions
Knowledge Check
The side length of a square inscribed in a circle is 2. what is the area of the circle?
AπB√2πC2πD2√2π
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.

View Solutionin the adjoining figure ABCD is a square of side 14 cm. Find the radius of the circle

View SolutionIn Figure, PQRS is a square of side 4 cm. Find the area of the shaded region.
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
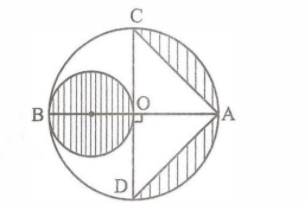
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View SolutionA square is inscribed in a circle of radius 7 cm. Find the area of the square.
View SolutionIn the given figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semi circles are drawn with AD and BC as diameters. Find the area of the shaded region
(Take π=227)
View Solution


