Combination of quadrilateral and circle : In Figure; ABCD is a trapezium with AB||DC ; AB = 18cm; DC = 32cm and the distance between AB and DC is 14 cm. Circles of Equal radii 7 cm with centres A;B;C and D have been drawn. Then; find the area of the shaded region of the figure.
To find the area of the shaded region in the trapezium ABCD with circles centered at its vertices, we will follow these steps:
Step 1: Calculate the Area of the Trapezium
The area A of a trapezium can be calculated using the formula:
A=12×(a+b)×h
where a and b are the lengths of the parallel sides, and h is the height (distance between the parallel sides).
Given:
- AB=18cm
- DC=32cm
- Distance between AB and DC=14cm
Substituting the values into the formula:
A=12×(18+32)×14
=12×50×14
=25×14=350cm2
Step 2: Calculate the Area of the Four Circular Sectors
Each circle has a radius r=7cm. The area of a full circle is given by:
Area of circle=πr2
The area of one sector (which is 14 of a circle) is:
Area of one sector=14×πr2
Thus, the area of four sectors is:
Area of four sectors=4×14×πr2=πr2
Substituting r=7:
Area of four sectors=π×72=π×49
Using π≈227:
Area of four sectors=227×49=154cm2
Step 3: Calculate the Area of the Shaded Region
The area of the shaded region is the area of the trapezium minus the area of the four sectors:
Area of shaded region=Area of trapezium−Area of four sectors
=350cm2−154cm2
=196cm2
Final Answer
The area of the shaded region is:
196cm2
The area A of a trapezium can be calculated using the formula:
A=12×(a+b)×h
where a and b are the lengths of the parallel sides, and h is the height (distance between the parallel sides).
- AB=18cm
- DC=32cm
- Distance between AB and DC=14cm
A=12×(18+32)×14
=12×50×14
=25×14=350cm2
Each circle has a radius r=7cm. The area of a full circle is given by:
Area of circle=πr2
The area of one sector (which is 14 of a circle) is:
Area of one sector=14×πr2
Thus, the area of four sectors is:
Area of four sectors=4×14×πr2=πr2
Substituting r=7:
Area of four sectors=π×72=π×49
Using π≈227:
Area of four sectors=227×49=154cm2
The area of the shaded region is the area of the trapezium minus the area of the four sectors:
Area of shaded region=Area of trapezium−Area of four sectors
=350cm2−154cm2
=196cm2
The area of the shaded region is:
196cm2
Topper's Solved these Questions
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 A
24 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 B
32 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Revision Exercise Long Answer Question
5 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
Similar Questions
In figure, ABCD is a trapezium with AB|| DC . AB = 18 cm, DC = 32 cm and distance between AB and DC= 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.

View SolutionIn figure arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region .

View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn Figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O . Find the area of the shaded region.
View SolutionIn the given figure, ABCD is a trapezium with angle C=120∘,DC=28 cm and BC=40 cm. Find :
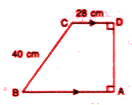
(i) AB
View SolutionIn figure, arcs have been drawn of radius 21 cm each with vertices A,B,C and D of quadrilateral ABCD as centres . Find the area of the shaded region.

View SolutionConstructed a parallelogram ABCD, when :
AB=4.5cm,∠B=120∘ and the distance between AB and DC = 3.0cm.
View SolutionIn the following figure, ABCD to a trapezium with AB // DC. If AB=9cm,DC=18cm,CF=13.5cm,AP=6cmandBE=15cm
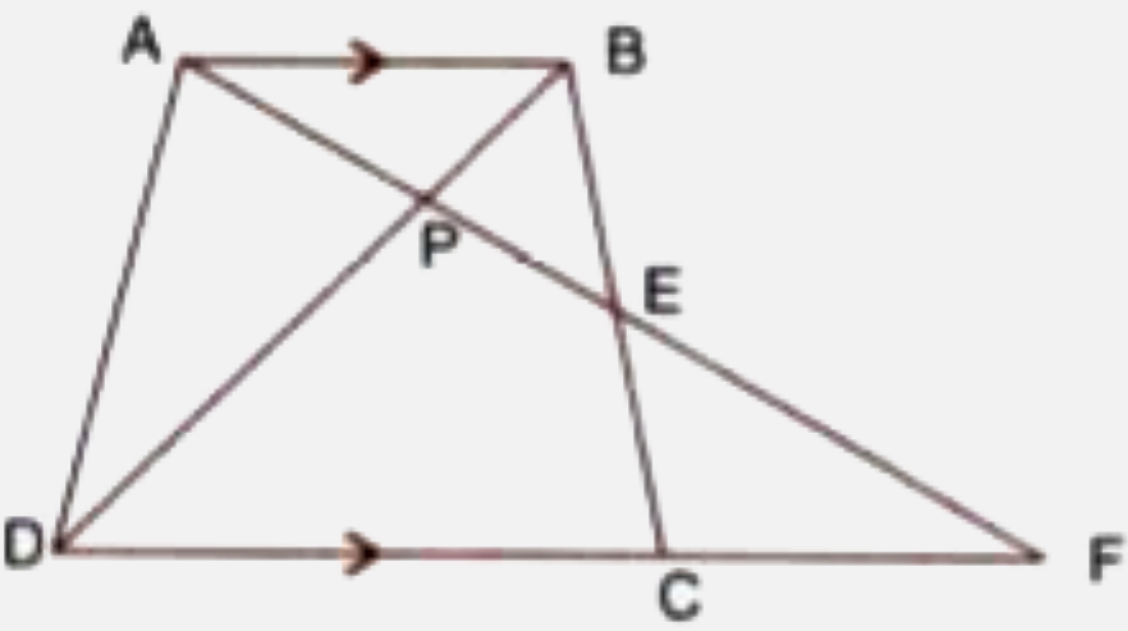
Calculate
EC
View SolutionIn the following figure, ABCD to a trapezium with AB // DC. If AB=9cm,DC=18cm,CF=13.5cm,AP=6cmandBE=15cm

Calculate
AF
View SolutionIn the following figure, ABCD to a trapezium with AB // DC. If AB=9cm,DC=18cm,CF=13.5cm,AP=6cmandBE=15cm

Calculate
PE
View Solution
