Smaller area enclosed by the circle x2+y2=4 and the line x+y=2 is:
2(π−2)
π−2
2π−1
2(π+2)
The correct Answer is:B
The smaller bounded by the circle x2+y2=4 and the line x+y=2 is shown by the shaded region ACBA.
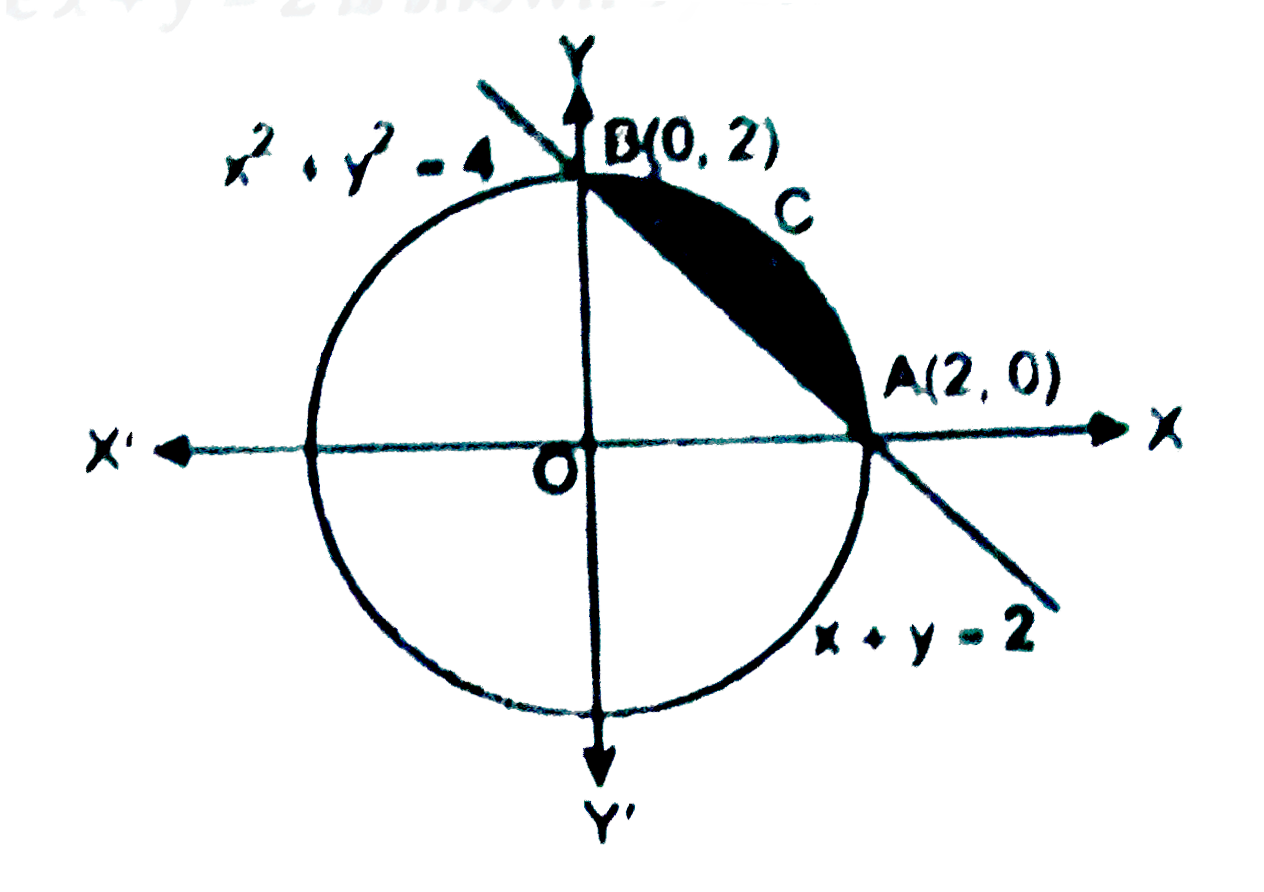
The points of intersection of the circle and line are A(2, 0) and B(0, 2).
∴ Required area (shaded region).
=ar(OACBO)−ar(△OAB)
=∫20√4−x2dx−∫20(2−x)dx
=[x2√4−x2+42sin−1x2]20−[2x−x22]20
=[22√4−4+42sin−1(1)−0−42sin−1(0)]−[4−2]
=[2⋅π2]−[4−2]=(π−2) sq. units.
Topper's Solved these Questions
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise
19 Videos
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.1
13 Videos
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise
24 Videos
- Continuity and DifferentiabilityBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise
23 Videos
Similar Questions
Find the area enclosed by the circle x2+y2=a2.
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4 and the lines x=0 and x=2 is:
View SolutionThe area enclosed by the curve y2+x4=x2 is
View SolutionFind the area enclosed between the circle x2+y2=25 and the straight line x+y=5.
View SolutionThe area bounded by the circle x2+y2=a2 and the line x+y=a in the first quadrant is
View SolutionThe area of the region bounded by the circle x2+y2=1 and the line x+y=1 is :
View SolutionFind the area enclosed between the parabola y2=4axand the line y=mx.
View SolutionFind the area enclosed by the curve y=−x2 and straight line x+y+2=0.
View SolutionThe area enclosed between the curves y2=xandy=|x| is
View SolutionIf (−2a,a+1) lies in the interior (smaller region) bounded by the circle x2+y2=4 and the parabola y2=4x, then
View Solution
