Find the area bounded by curves (x−1)2+y2=1and x2+y2=1.
Video Solution
Text Solution
Curve (x−1)2+y2=1 …(1)
∴y=√1−(x−1)2
Represents a circle whose centre is (1, 0) and radius is 1.
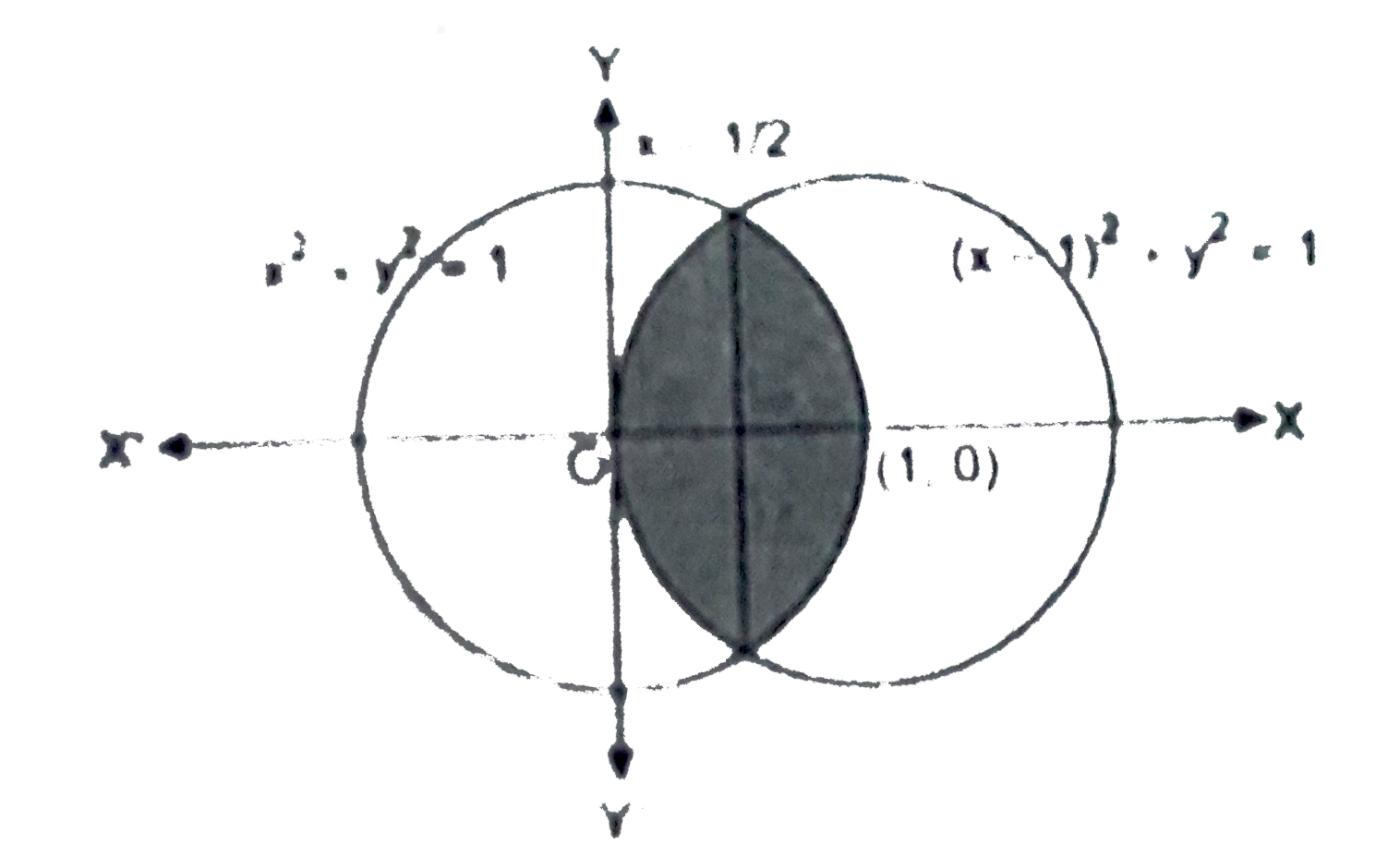
and curve, x2+y2=1 ...(2)
∴y=√1−x2
Represents a circle whose centre is (0, 0) and radius is 1.
Two circles meet at (x−1)2=x2
⇒2x=1⇒x=12
∴ Required area (shaded region)
=2[∫1/20y1dx+∫11/2y2dx]
=2[∫1/20√1−(x−1)2dx+∫11/2√1−x2dx]
=2[x−12√1−(x−1)2+12sin−1x−11]1/20+2[x2√1−x2+12sin−1x]11/2
=2⎡⎣12−12√1−14+12sin−1(−12)−(−12)0−12sin−1(−1)⎤⎦+2[0+12sin−1(1)−14√1−14−12sin−112]
=2[−14⋅√32−12⋅π6+0+12⋅π2]+π2−12⋅√32−π6
=−√34−π6+π2+π2−√34−π6
=(2π3−√32) sq. units.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise19videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.113videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise24videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise23videos
Continuity and Differentiability
Similar Questions
Find the area bounded by the curves x+2|y|=1 and x=0 .
View SolutionFind the area bounded by the curves x+2|y|=1 and x=0 .
View SolutionFind the area bounded by curves −4y2=x and x=1+5y2
View SolutionFind the area bounded by the curves x2=y, x2=−y and y2=4x−3
View SolutionFind the area bounded by the curves x=y2 and x=3−2y2.
View SolutionFind the area bounded by the curve |x|+y=1 and axis of x.
View SolutionFind the area bounded by the curves y=ex,y=|x−1| and x=2.
View SolutionFind the area bounded by the curves x=∣∣y2−1∣∣ and y=x−5
View SolutionFind the area bounded by the curves y=6x−x2andy=x2−2x
View SolutionFind the area bounded by the curves x2+y2=4,x2=−√2y and x=y
View Solution
