Find the area of circle 4x2+4y2=9 which is interior to the parabola x2=4y
Given equation of circle is 4x2+4y2=9 and equation of parabola is x2=4y.
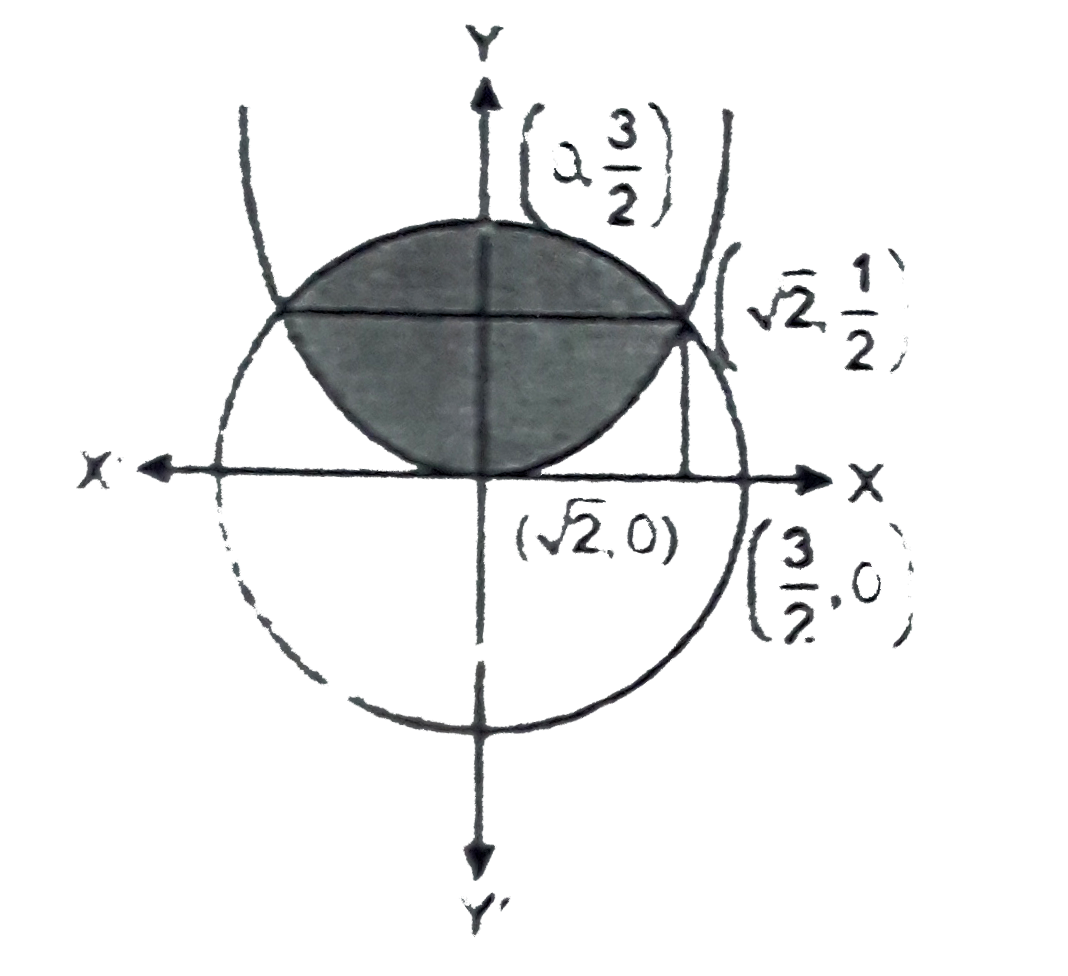
Now, solving the equations of two curves,
4(4y)+4y2=9
⇒4y2+16y−9=0
⇒y=−16±√256+1442×4
=−16±√4008
=−16±208=12,−92
but y gt 0, so two curves will meet when y=12,
∴x2=4×12=2
⇒x=±√2
∴ Required area=2∫√20(y2−y1)dx
={∫√20√9−4x24dx−∫√20x24dx}
=2∫√20√(32)2−x2dx−24[x33]√20
=2⎡⎣x2√(32)2−x2+(3/2)22sin−1(x3/2)⎤⎦√20−16[(√2)3−0]
=[x√94−x2+94sin−1(2x3)]√20−2√26
=[√2√94−2+94sin−1(2√23)]−{0−0}−2√26
=√22+94sin−1(2√23)−2√26
=(√22−√23)+94sin−1(2√23)
=√26+94sin−1(2√23) sq. units.
Topper's Solved these Questions
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise
19 Videos
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.1
13 Videos
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise
24 Videos
- Continuity and DifferentiabilityBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise
23 Videos
Similar Questions
Find the equation of line which is normal to the parabola x2=4y and touches the parabola y2=12x.
View SolutionThe largest value of a for which the circle x2+y2=a2 falls totally in the interior of the parabola y2=4(x+4) is 4√3 (b) 4 (c) 4√67 (d) 2√3
View SolutionFind the area of the region which is inside the parabola y=−x2+6x−5, outside the parabola y=−x2+4x−3 and left of the straight line y=3x−15.
View SolutionFind the equation of the circle which is concentric with the circle x2+y2−4x+6y−3=0 and the double of its area.
View SolutionFind the radius of the largest circle, which passes through the focus of the parabola y2=4(x+y) and is also contained in it.
View SolutionIf the circle x2+y2+2ax=0,a∈R touches the parabola y2=4x, them
View SolutionFind the equation of the circle which cuts each of the circles x2+y2=4, x2+y2−6x−8y.+10=0 & x2+y2+2x−4y−2=0 at the extremities of a diameter
View SolutionIf (−2a,a+1) lies in the interior (smaller region) bounded by the circle x2+y2=4 and the parabola y2=4ax, then find the values of a
View SolutionIf (−2a,a+1) lies in the interior (smaller region) bounded by the circle x2+y2=4 and the parabola y2=4x, then
View SolutionThe number of points with integral coordinates that lie in the interior of the region common to the circle x2+y2=16 and the parabola y2=4x, is
View Solution
