Find the area bounded by the curve $x^{2} = 4 y$ and the straight line $x = 4 y - 2 .$

Video Solution

Text Solution

Verified by Experts

$x^{2} = 4 y \Rightarrow y = \frac{x^{2}}{4}$ ...(1)
$x = 4 y - 2 \Rightarrow y = \frac{x + 2}{4}$ ...(2)
The points of intersection of the parabola and straight line are C(2, 1) and $D (- 1, \frac{1}{4})$ .

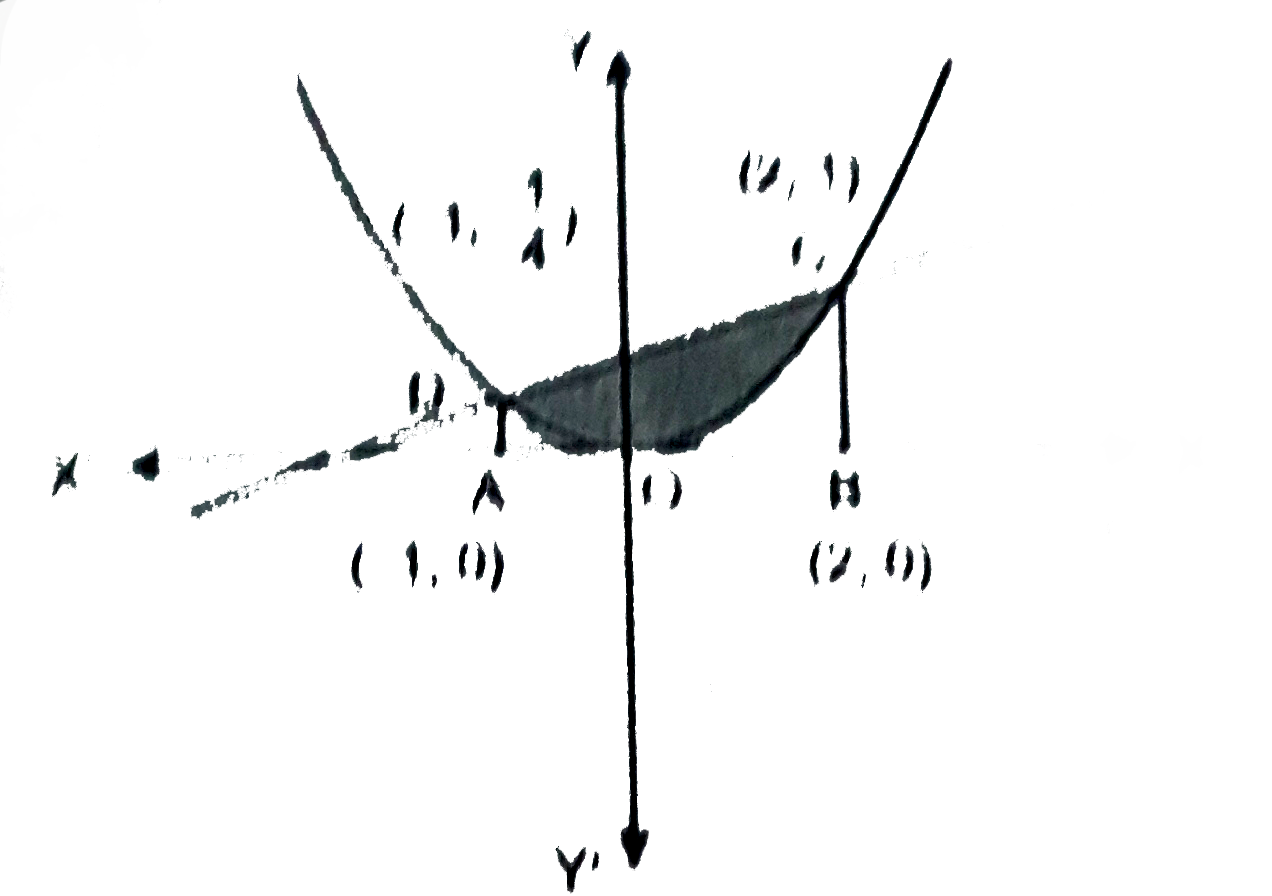
Draw the graph of both curves.
Required area = area of ABCDA - area of ABCODA
$= \int_{- 1}^{2} \frac{x + 2}{4} d x - \int_{- 1}^{2} \frac{x^{2}}{4} d x$
$= \frac{1}{4} {[\frac{x^{2}}{2} + 2 x]}_{- 1}^{2} - \frac{1}{4} {[\frac{x^{3}}{3}]}_{- 1}^{2}$
$= \frac{1}{4} [(2 + 4) - (\frac{1}{2} - 2)] - \frac{1}{12} [8 - (- 1)]$
$= \frac{1}{4} (6 + \frac{3}{2}) - \frac{1}{2} \times 9$
$= \frac{15}{8} - \frac{3}{4} = \frac{9}{8} \times 9$ sq. units.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF INTEGRALS-Exercise 8.1

Home
Ask Doubt
Profile