Find area enclosed by ellipse $\frac{x^{2}}{16} + \frac{y^{2}}{9} = 1$

Video Solution

Text Solution

Verified by Experts

Given curve is an ellipse which is symmetric about X-axis both, as shown in the figure.

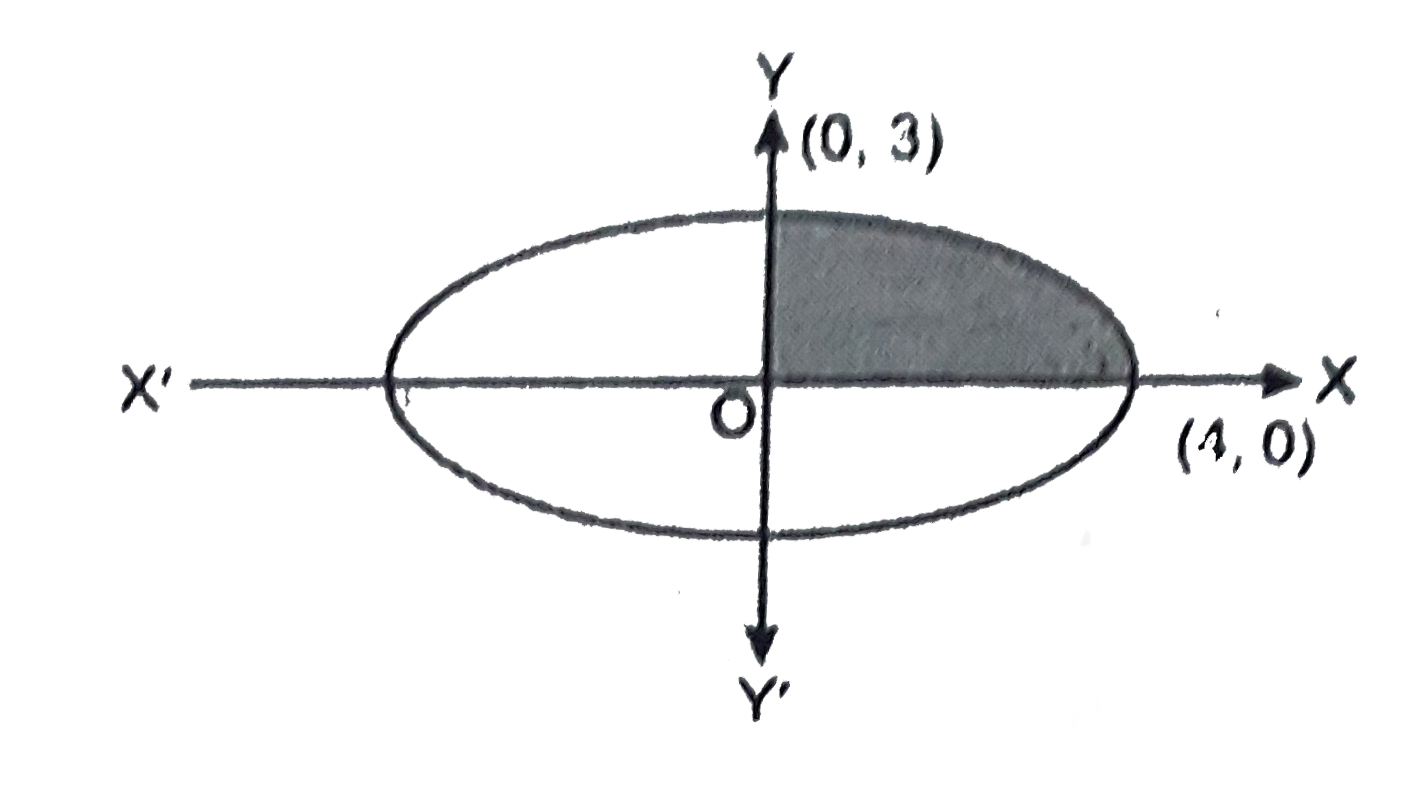
$∴$ Area bounded by ellipse
$= 4 \times$ (area of shaded region in first quadrant)
$= 4 \times \int_{0}^{4} y d x$
$= 4 \int_{0}^{4} \frac{3}{4} \sqrt{16 - x^{2}} d x$
$= 3 \cdot \int_{0}^{4} \sqrt{4^{2} - x^{2}} d x$
$= 3 {[\frac{x}{2} \sqrt{4^{2} - x^{2}} + \frac{4^{2}}{2} {sin}^{- 1} (\frac{x}{4})]}_{0}^{- 1}$
$= 3 [2 \sqrt{16 - 16} + 8 {sin}^{- 1} (1) - 0 - 8 {sin}^{- 1} (0)]$
$= 3 [0 + 8 {sin}^{- 1} (1) - 0]$
$= 3 \times 8 \times (\frac{π}{2}) = 12 π$ sq. units.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF INTEGRALS-Exercise 8.1

Home
Ask Doubt
Profile