P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD such that AC ⊥ BD. Prove that PQRS is a rectangle.
Given, ABCD is a rhombus and P, Q, R and S are mid-points of AB, BC, CD and DA.
∴ by mid-point theorem,
InΔADC, SR||ACandSR=12AC ...(1)
InΔABC, PQ||ACandPQ=12AC ...(2)
From (1) and (2), we get
PQ||SRandPQ=SR=12AC
∴PQRSis a parallelogram. (∵one pair of opposite sides is equal and parallel)
Now, we know that diagonals of a rhombus bisect each other at right angles.
∴ ∠EOF=90∘
Now, RQ||BD (by mid-point theorem)
⇒ RE||FO
Also, SR||AC [from (1)]
⇒ FR||OE
∴OERFis parallelogram. (∵pairs of opposite sides are parallel)
So, ∠ERF=∠EOF=90∘
(∵pairs of opposite sides are parallel)
Thus, PQRS is a parallelogram with ∠R=90∘.
Hence, PQRS is a rectangle.

Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Exercise 8b
Explore 15 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Revision Exercise (long Answer Questions)
Explore 5 Videos
- PROBABILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICSExercise:Revision Exercise
Explore 12 Videos
Similar Questions
P, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and AC⊥BD. Prove that PQRS is a square.
View SolutionABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionIf the sides of a quadrilateral ABCD touch a circle prove that
AB+CD=BC+AD.
View SolutionP,Q,R and S are the mid points of sides AB,BC , CD and DA respectively of rhombus ABCD. Show that PQRS is a rectangle.
Under what conditions will PQRS be a square ?
View SolutionP and Q are the mid-point of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PQRS is a parallelogram.

View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD.
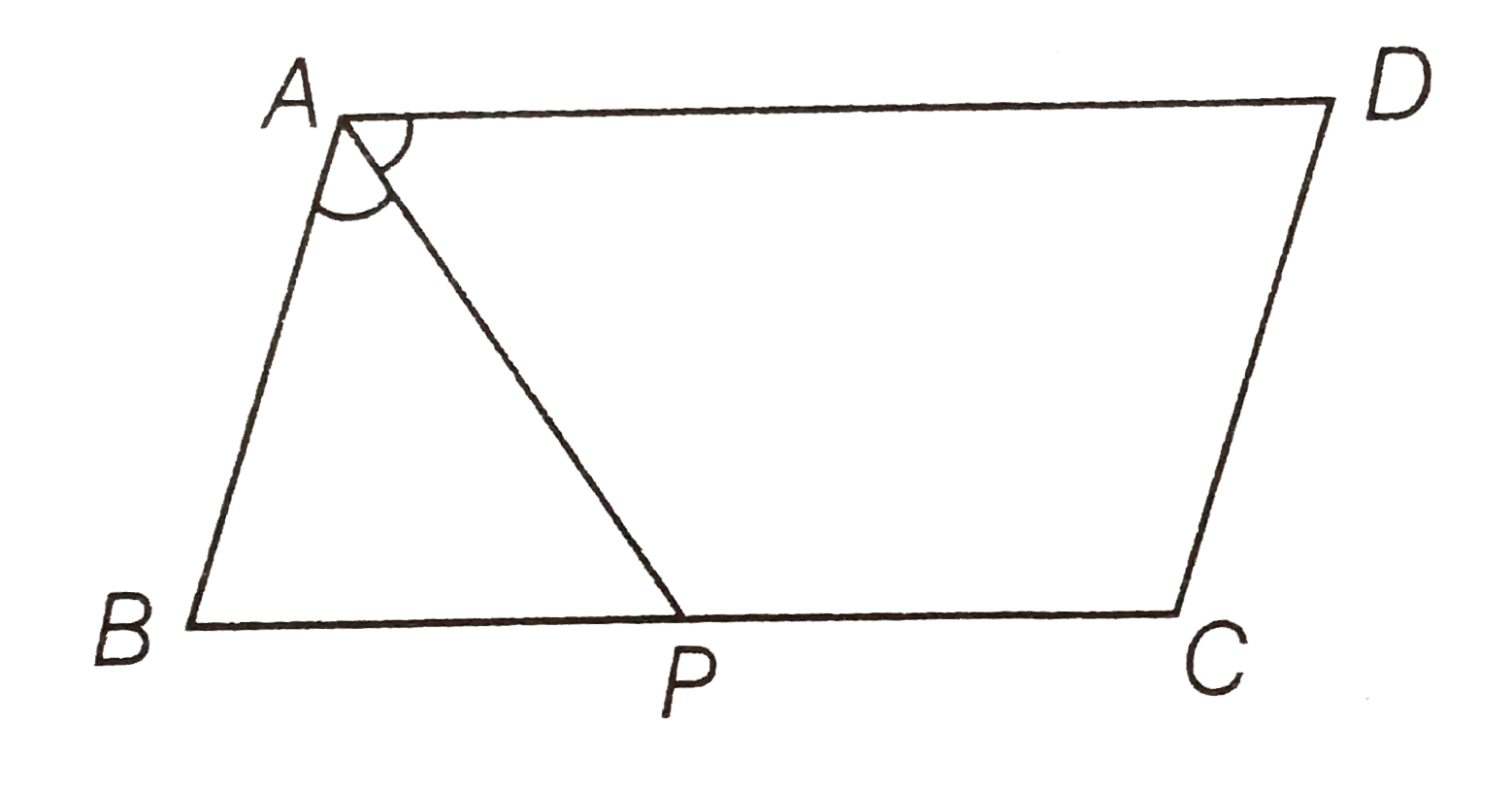
View SolutionShow that in a quadrilateral ABCD AB+BC+CD+DA>AC+BD
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that : (i) SR ∣∣ AC and SR=12AC (ii) PQ=SR (iii) PQRS is a parallelogram
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View Solution

