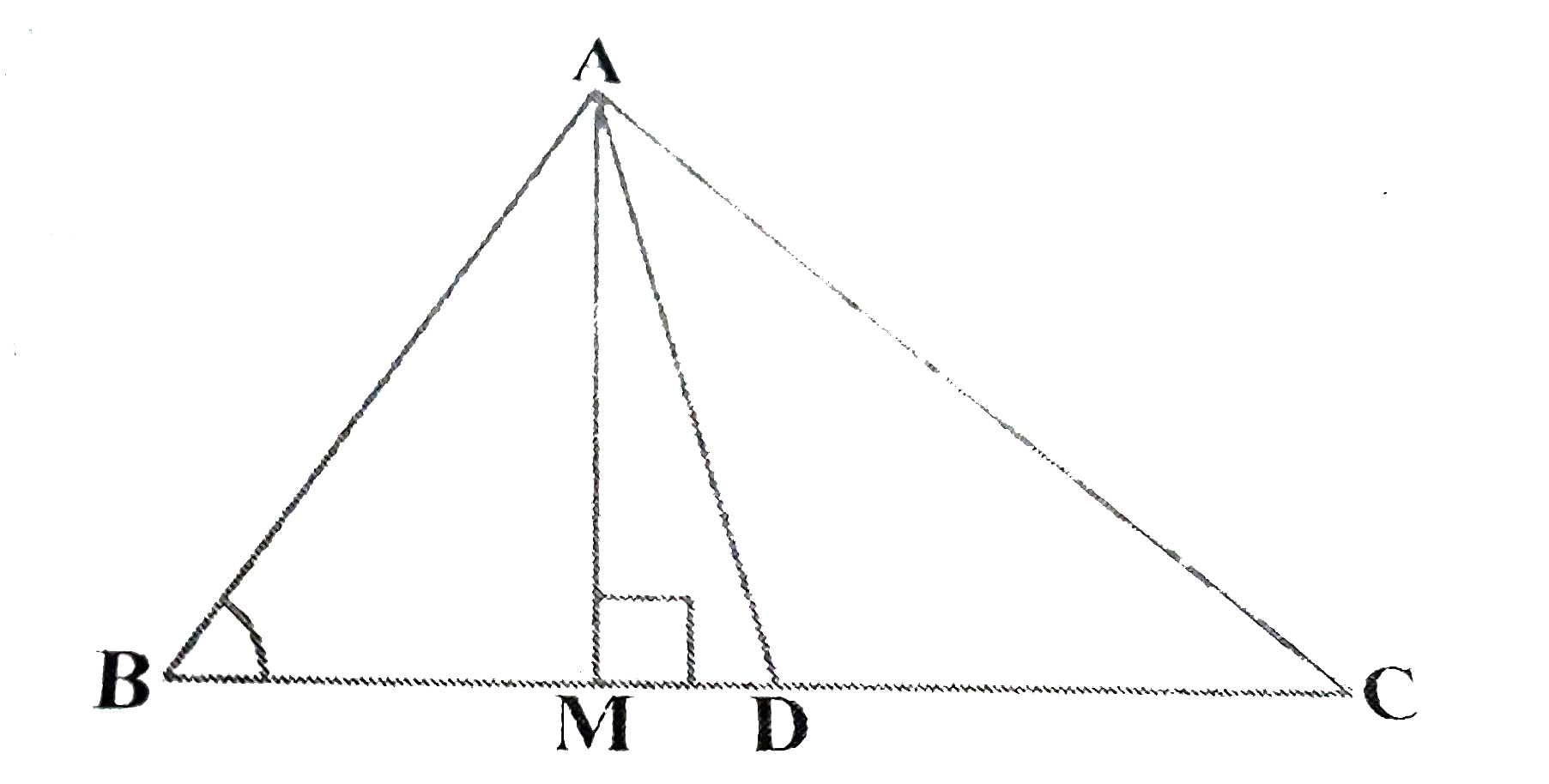
आकृति 6.60 में AD त्रिभुज ABC कि एक माधियाका हैं तथा AM⊥BC हैं। सिध्य कीजिये कि
i) AC2=AD2+BC.DM+(BC2)2
ii) AB2=AD2−BC.DM+(BC2)2
iii) AC2+AB2=2AD2+12BC2
Step by step video solution for आकृति 6.60 में AD त्रिभुज ABC कि एक माधियाका हैं तथा AM bot BC हैं। सिध्य कीजिये कि i) AC^(2)=AD^(2)+BC.DM + ((BC)/2)^(2) ii) AB^(2)=AD^(2)-BC.DM+((BC)/2)^(2) iii) AC^(2)+AB^(2)=2AD^(2)+1/2BC^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुजBook:DEEPAK PUBLICATIONChapter:त्रिभुजExercise:बहुविकल्पीय-प्रश्न
Explore 58 Videos
- त्रिभुजBook:DEEPAK PUBLICATIONChapter:त्रिभुजExercise:परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न
Explore 21 Videos
- त्रिभुजBook:DEEPAK PUBLICATIONChapter:त्रिभुजExercise:प्रश्नावली 6.5
Explore 20 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग Book:DEEPAK PUBLICATIONChapter:त्रिकोणमिति के कुछ अनुप्रयोग Exercise:अभ्यास के लिए प्रश्न
Explore 14 Videos
- दो चार वाले रैखिक समीकरण युग्म Book:DEEPAK PUBLICATIONChapter:दो चार वाले रैखिक समीकरण युग्म Exercise:अभ्यास के लिए प्रश्न
Explore 74 Videos
Similar Questions
यदि दो त्रिभुजों में संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) होती हैं और इसलिए ये समरूप होते हैं। सिद्ध करें।
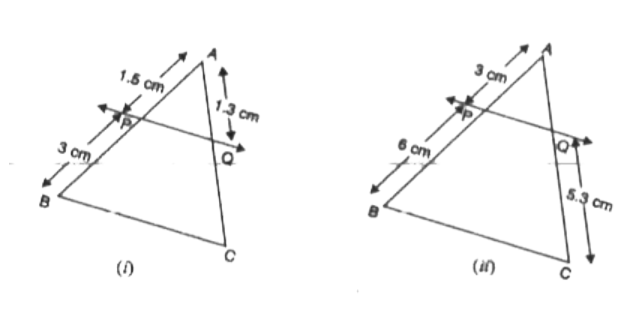
View Solutionयदि आकृति (1) और (i) में, PQ || BC हो, तो (i) में QC और (ii) में AQ ज्ञात कीजिए-
View Solutionयदि किसी समकोण त्रिभुज के समकोण वाले शीर्ष से कर्ण पर लंब डाला जाए तो इस लंब के दोनों ओर बने त्रिभुज संपूर्ण त्रिभुज के समरूप होते हैं तथा परस्पर भी समरूप होते हैं।
View Solutionकिसी ऊर्ध्वाधर मीनार के पाद बिन्दु से 20 मीटर दूर धरती पर एक बिन्दु से मीनार के शिखर का उन्नयन कोण 60∘है | मीनार की ऊँचाई क्या है ?
View Solutionदो रेल पटरियां , समीकरणों x+2y−4=0 और 2x+4y−12=0 द्वारा निरूपित की गई है| इस स्थिति को ज्यामितीय रूप से व्यक्त कीजिए।
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCDE+14BC2 (ii) AB2+AC2=2 AD2+12BC2
View Solutionआकृति 6.60 में AD त्रिभुज ABC कि एक माधियाका हैं तथा AM⊥BC हैं। सिध्य कीजिये कि
i) AC2=AD2+BC.DM+(BC2)2
ii) AB2=AD2−BC.DM+(BC2)2
iii) AC2+AB2=2AD2+12BC2

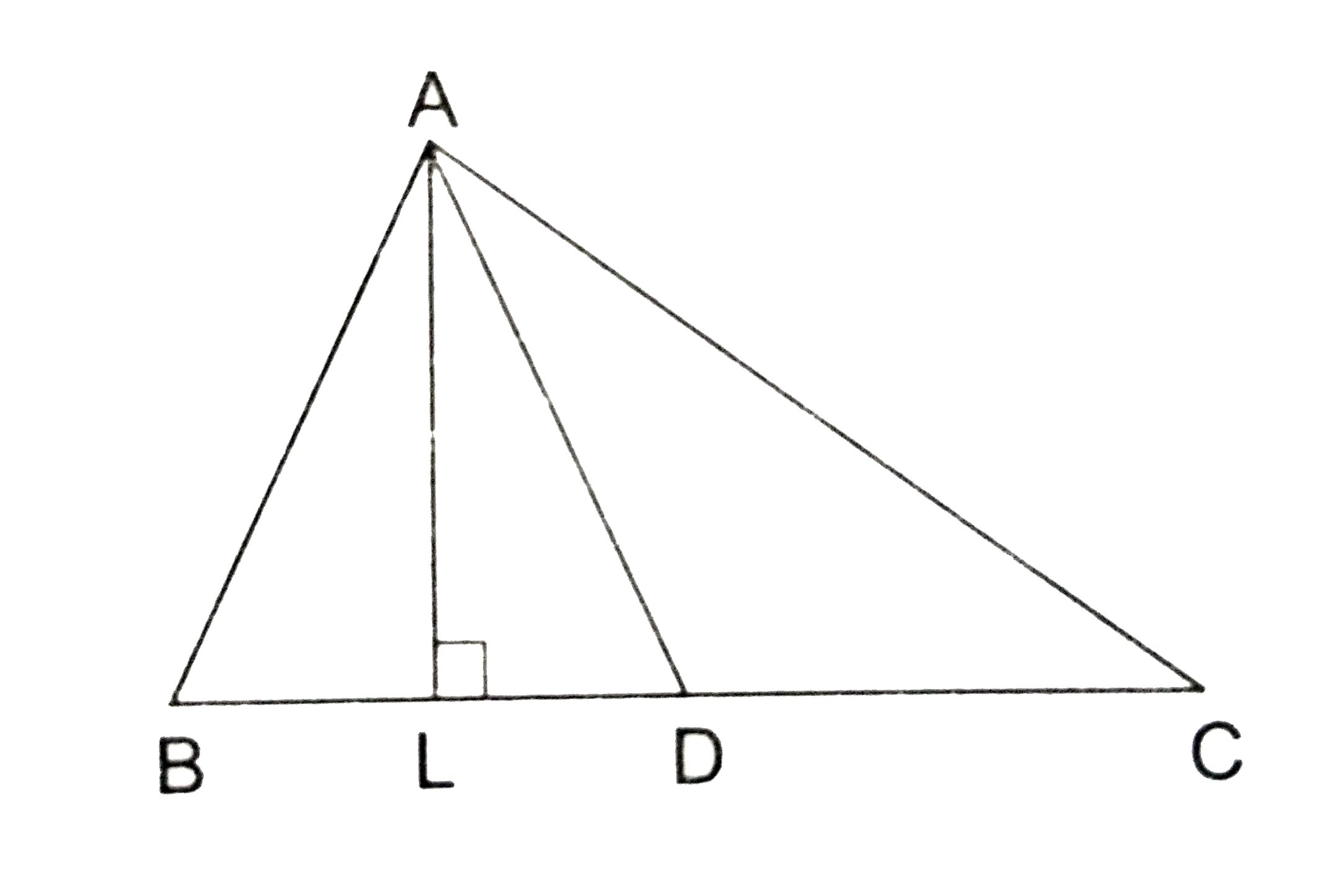
View SolutionIn aΔABC,AD is a median and AL⊥BC.
Prove that
(a) AC2=AD2+BC⋅DL+(BC2)2
(b) AB2=AD2−BC⋅DL+(BC2)2
(c) AC2+AB2=2AD2=2AD2+12BC2
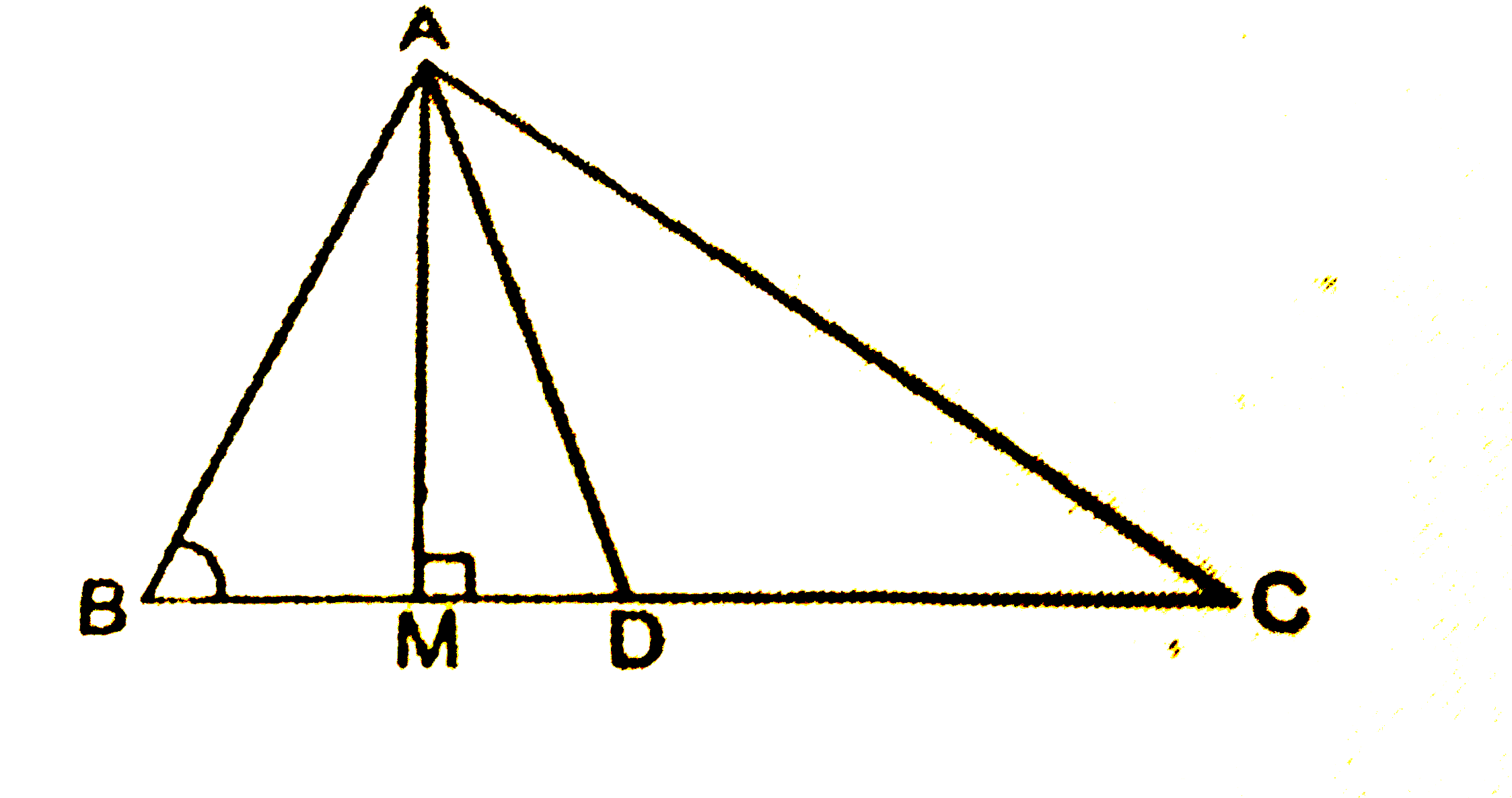
View Solutionआकृति में AD त्रिभुज ABC की एक माध्यिका है तथा AM⊥BC है । सिद्ध कीजिए कि
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
View Solutionएक △ABC में, AC>BD है | D, BC का मध्य बिन्दु है तथा AE⊥BC तो सिद्ध कीजिए कि :
(i) AC2=AD2+BC⋅DE+14BC2
(ii) AB2=AD2−BC⋅DE+14BC2
View SolutionIn ΔABC, AD is a median and AM⊥ BC.Prove that
(a) AC2=AD2+BC.DM+(BC2)2 (b) AB2=AD2−BC.DM+(BC2)2 (c ) AC2+AB2=2AD2+12BC2
View SolutionIn Fig . AD is a median of a triangle ABDandAM⊥BC. Prove that :
AB2=AD2−BC.DM+(BC2)2
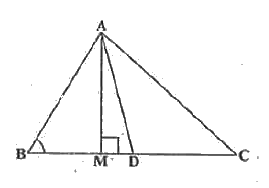
View SolutionIn Fig . AD is a median of a triangle ABDandAM⊥BC. Prove that :
AC2+AB2=2AD2+12BC2
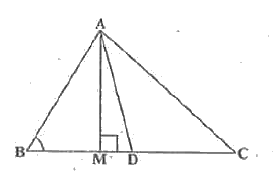
View SolutionIn Fig . AD is a median of a triangle ABDandAM⊥BC. Prove that :
AC2+AB2=2AD2+12BC2

View SolutionIn the given figure, ABC is a Deltain which ∠ABC<90∘ and AD⊥BC. Prove that AC2=AB2+BC2−2BC⋅BD
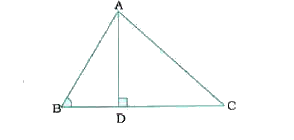
View SolutionIn the given figure, AD is a median of a DeltaABC and AM⊥BC. Prove that :
AC2+AB2=2AD2+12BC2
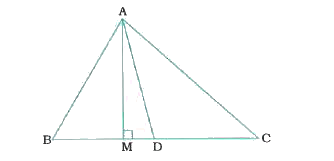
View Solution

