Choose the option showing the correct match for work done by n moles of a diatomic ideal gas for change in temperature in different processes.
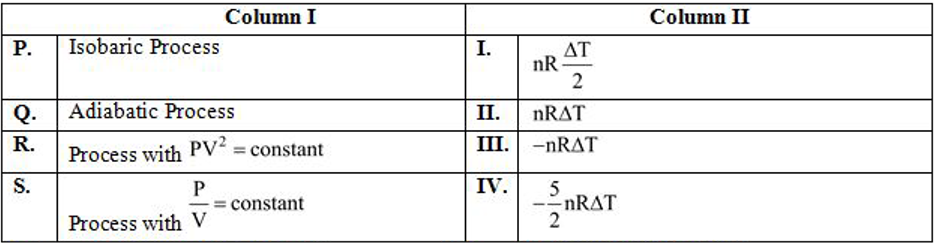
[P−II][Q−III][R−II][S−III]
[P−II][Q−IV][R−III][S−II]
[P−III][Q−IV][R−II][S−I]
[P−II][Q−IV][R−III][S−II]
The correct Answer is:B
For isobaric process: W=PΔV=nRΔT
For adiabotic process: W=−ΔU=−nCVΔT=−52nRΔT
For a polytropic process PVx= constant
C=CV−Rx−1
Multiplying by nΔT
nCΔT=nCVΔT−nRΔTx−1
As nCΔT=ΔQandnCVΔT=ΔU
∴W=−nRΔTx−1(As ΔQ=DU+W)
For PV2= constant, x=2
∴W=−nRΔT2−1=−nRΔT
For PV= constant, x=−1
∴W=−nRΔT−1−1=nRΔT2
Topper's Solved these Questions
- MOCK TEST 3BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 3EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
- MOCK TEST 2BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 2EXERCISE - PART I : PHYSICS (SECTION - 2)
10 Videos
- MOCK TEST 4BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 4EXERCISE - PHYSICS (SECTION 2)
5 Videos
Similar Questions
The ratio of work done by an ideal diatomic gas to the heat supplied by the gas in an isobatic process is
View SolutionThe work done by 1 mole of ideal gas during an adiabatic process is (are ) given by :
View SolutionDefine an adiabatic process and state essential conditions for such a process to take place. Write its process equations in terms of , and . Show analytically that work done by one mole of an ideal gas during adiabatic expansion from temperature T1 to T2 is given by =R(T1−t2)1−λ.
View SolutionFor a diatomic gas, which options is/are correct?
View SolutionOne mole of an ideal gas undergoes a process whose molar heat capacity is 4R and in which work done by gas for small change in temperature is given by the relation dW=2RdT, then find the degree of freedom of gas
View SolutionState true or false. Work done by an ideal gas in adiabatic expansion is less than that in isothermal process (for same temperature range)
View SolutionAn ideal monatomic gas undergoes a process where its pressure is inversely proportional to its temperature.
(a) Calculate the molar specific heat of the process.
(b) Find the work done by two moles of gas if the temperature change from T1 to T2.
View SolutionFor one mole of a diatomic gas, the ratio of heat transfer at constant pressure to work done by the gas is
View SolutionAn ideal gas undergoes an isobaric process. If its heat capacity is C, at constant volume and number of mole n, then the ratio of work done by gas to heat given to gas when temperature of gas changes by ΔT is :
View Solutionn moles of diatomic gas in a cylinder is at a temperature T . Heat is supplied to the cylinder such that the temperature remains constant but n moles of the diatomic gas get converted into monatomic gas . The change in the total kinetic energy of the gas is
View Solution
