The ratio of work done by an ideal diatomic gas to the heat supplied by the gas in an isobatic process is
The correct Answer is:C
To solve the problem of finding the ratio of work done by an ideal diatomic gas to the heat supplied by the gas in an isobaric process, we can follow these steps:
Step 1: Understand the First Law of Thermodynamics
The first law of thermodynamics states:
W=Q−ΔU
where:
- W is the work done by the gas,
- Q is the heat supplied to the gas,
- ΔU is the change in internal energy.
Step 2: Express Work Done and Heat Supplied
For an ideal gas, the work done W in an isobaric process can be expressed as:
W=nCpΔT−nCvΔT
where:
- n is the number of moles,
- Cp is the specific heat at constant pressure,
- Cv is the specific heat at constant volume,
- ΔT is the change in temperature.
Step 3: Substitute Values for Diatomic Gas
For a diatomic ideal gas:
- Cp=72R
- Cv=52R
Substituting these values into the equation for work done:
W=n(72RΔT−52RΔT)
W=nRΔT
Step 4: Calculate Heat Supplied
The heat supplied Q in an isobaric process is given by:
Q=nCpΔT
Substituting the value of Cp:
Q=n(72R)ΔT
Q=72nRΔT
Step 5: Find the Ratio of Work Done to Heat Supplied
Now, we need to find the ratio WQ:
WQ=nRΔT72nRΔT
The nRΔT terms cancel out:
WQ=172=27
Final Answer
Thus, the ratio of work done by the ideal diatomic gas to the heat supplied by the gas in an isobaric process is:
WQ=27
The first law of thermodynamics states:
W=Q−ΔU
where:
- W is the work done by the gas,
- Q is the heat supplied to the gas,
- ΔU is the change in internal energy.
For an ideal gas, the work done W in an isobaric process can be expressed as:
W=nCpΔT−nCvΔT
where:
- n is the number of moles,
- Cp is the specific heat at constant pressure,
- Cv is the specific heat at constant volume,
- ΔT is the change in temperature.
For a diatomic ideal gas:
- Cp=72R
- Cv=52R
W=n(72RΔT−52RΔT)
W=nRΔT
The heat supplied Q in an isobaric process is given by:
Q=nCpΔT
Substituting the value of Cp:
Q=n(72R)ΔT
Q=72nRΔT
Now, we need to find the ratio WQ:
WQ=nRΔT72nRΔT
The nRΔT terms cancel out:
WQ=172=27
Thus, the ratio of work done by the ideal diatomic gas to the heat supplied by the gas in an isobaric process is:
WQ=27
Similar Questions
For an ideal diatomic gas:
View SolutionIf heat is supplied to an ideal gas in an isothermal process.
View Solutiongraph of an ideal gas is as shown in figure.
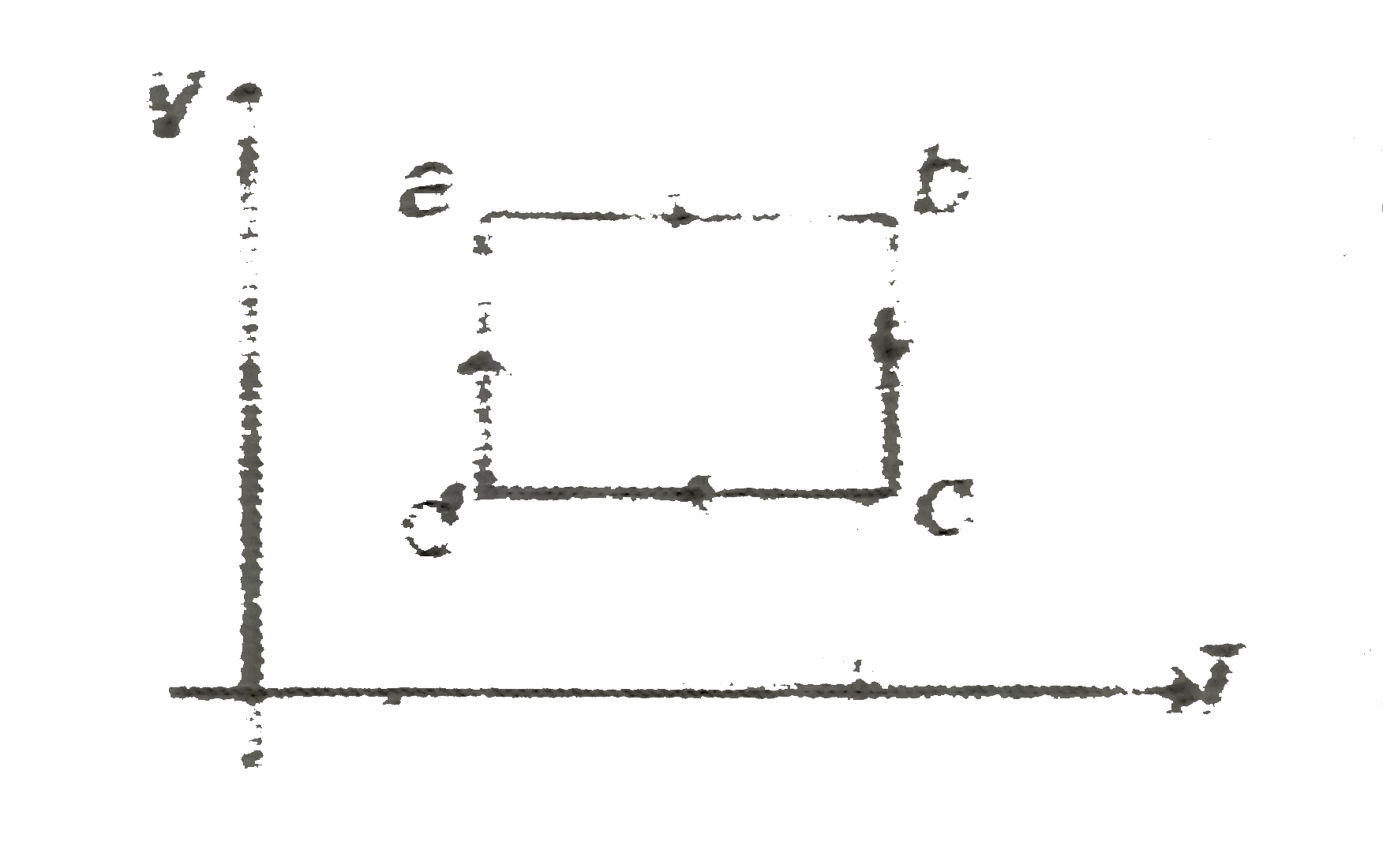
Heat is supplied to the gas in process (s).
View SolutionIn a isobaric process the work done by a di-atomic gas is 10 J , the heat given to the gas will be :
View SolutionAn insulator container contains 4 moles of an ideal diatomic gas at temperature T. Heat Q is supplied to this gas, due to which 2 moles of the gas are dissociated into atoms but temperature of the gas remains constant. Then
View SolutionChoose the option showing the correct match for work done by n moles of a diatomic ideal gas for change in temperature in different processes.
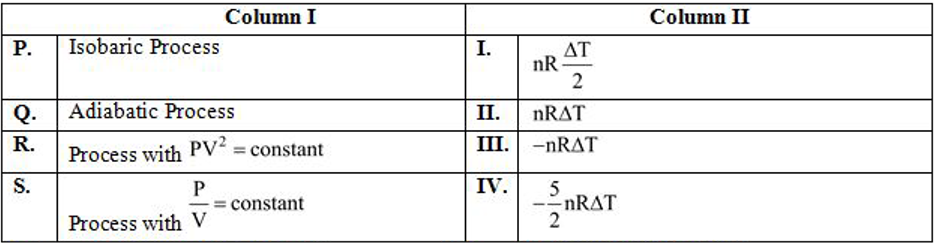
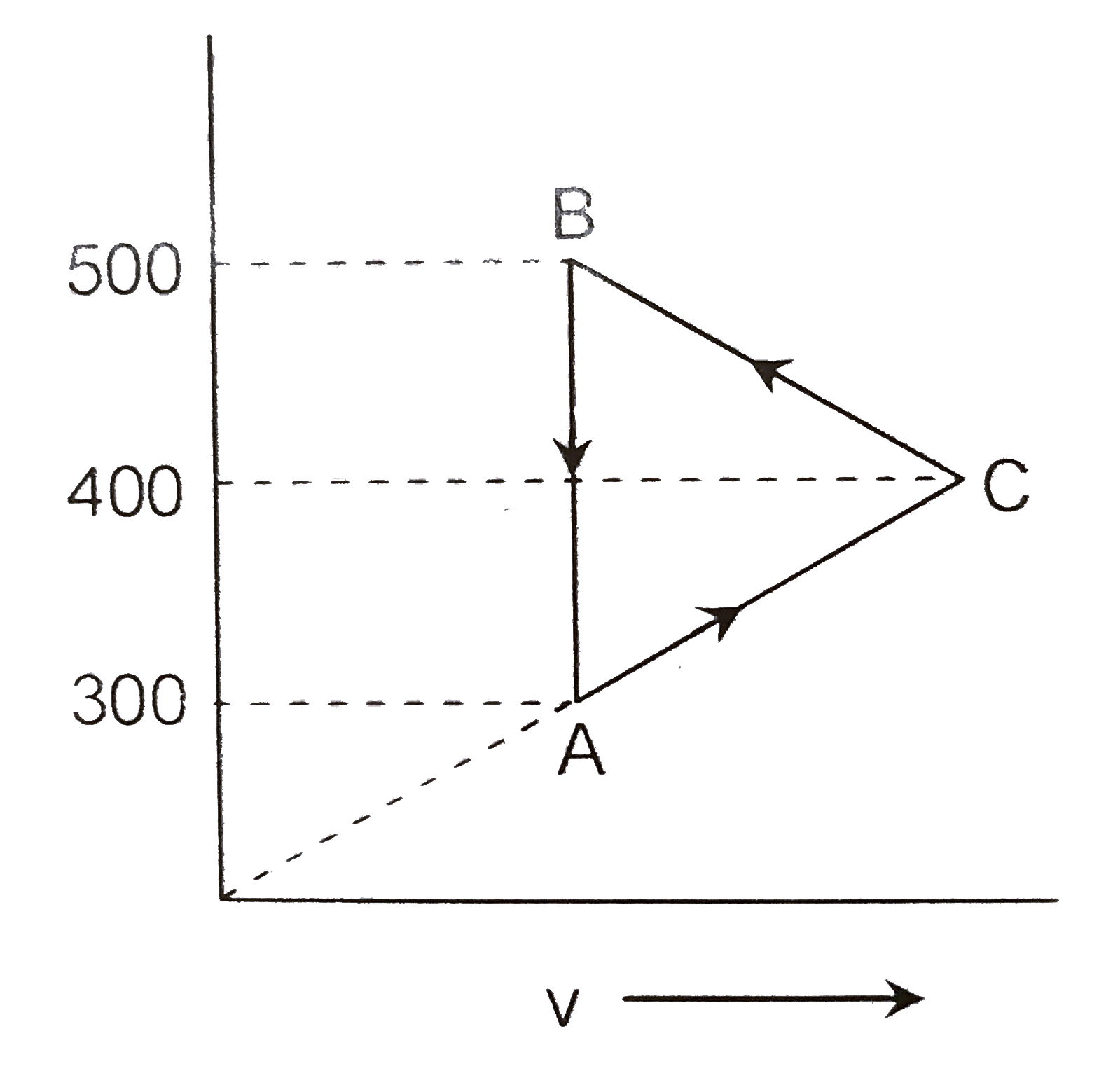
View SolutionWhat will be the work done in process CB for 1mol of an ideal gas if total 600 call heat is released by the gas in whole process.
View SolutionLet QandW denote the amount of heat given to an ideal gas and the work done by it in an adiabatic process.
View SolutionAssertion : For an isothermal process in an ideal gas, the heat obsorbed by the gas is entirely used in the work done by the gas.
Reason : During a process taking place in a system, the temperature remains constant then the process is isothermal.
View SolutionA diatomic gas (γ=1.4) does 200 J of work when it is expanded isobarically. Find the heat given to the gas in the process.
View Solution
