Three identical thin rods, each of mass m and length l, are joined to form an equilateral triangular frame. Find the moment of inertia of the frame about an axis parallel to its one side and passing through the opposite vertex. Also find its radius of gyration about the given axis.
v2MAX=4ga√3
v2MAX=√3 ga
v2MAX=2ga√3
v2MAX=ga√3
The correct Answer is:C
Using parallel axis theorem for the side BC, the moment of inertia of the triangle about an axis passing through A and perpendicular to the plane of the triangle,
IA=2(13ma2)+⎛⎝112ma2+m(√3a2)2⎞⎠=32ma2
If the angular velocity of the triangle at any instant is ω, the velocity of the vertex B at that instant is aω
Therefore, the velocity of B is maximum at the instant the angular velocity is maximum, i.e. when the side BC becomes horizontal
Let the angular velocity at this instant be ωMAX
Then, by conservation of energy
Gain in kinetic energy = Loss in potential energy
12IAω2MAX=3mg (Loss in height of CM of triangle)
12(32ma2)ω2MAX=3mg(a√3−a2√3)=√32mga ⇒ ω2MAX=2g√3a
Therefore, the maximum velocity of the vertex B is given by v2MAX=ω2MAXa2=2ga√3
Topper's Solved these Questions
- MOCK TEST 1Book:VMC MODULES ENGLISHChapter:MOCK TEST 1Exercise:PART I : PHYSICS (SECTION-2)
Explore 10 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Advanced (Archive)
Explore 78 Videos
- MOCK TEST 10Book:VMC MODULES ENGLISHChapter:MOCK TEST 10Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
Similar Questions
Three identical rods each of mass M, length l are joined to form an equilateral ΔABC . Find the Moment of Inertia about BC as shown.
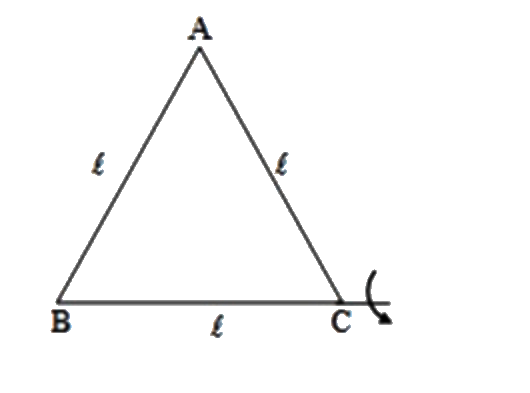
View SolutionFour thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View SolutionThree identical rods, each of mass m and length l, form an equaliteral triangle. Moment of inertia about one of the sides is

View SolutionFour identical thin rods each of mass M and length l, from a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.

View SolutionFour identical uniform thin rods, each of mass m and length l are joined to a common point O as shown in the figure. Moment of inertia of the system about an axis passing through O and lying in the plane of rods is
View SolutionThree uniform rods, each of length 21 ( = 1m) and mass M = 8 kg are rigidly joined at their ends to form a triangular framework. Find the moment of inertia of the framework about an axis passing through the midpoints of two of its sides?
View SolutionConsider a uniform square plate of of side and mass m. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is -
View Solution