4μF capacitor is charged to 150 V and another capacitor of 6μF is charged to 200 V. Then they are connected across each other. Find the potential difference across them. Calculate the heat produced.
0.005J
0.500J
0.003J
1.003J
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Calculate the initial charge on each capacitor
The charge Q on a capacitor is given by the formula:
Q=C×V
For the first capacitor C1=4μF charged to V1=150V:
Q1=C1×V1=4×10−6F×150V=6×10−4C
For the second capacitor C2=6μF charged to V2=200V:
Q2=C2×V2=6×10−6F×200V=1.2×10−3C
Step 2: Calculate the total charge when connected
When the two capacitors are connected together, the total charge Qtotal is:
Qtotal=Q1−Q2=6×10−4C−1.2×10−3C=−6×10−4C
(Note: The negative sign indicates that the second capacitor has more charge than the first.)
Step 3: Calculate the equivalent capacitance
The equivalent capacitance Ceq when capacitors are connected in parallel is:
Ceq=C1+C2=4μF+6μF=10μF=10×10−6F
Step 4: Calculate the final voltage across the capacitors
The final voltage Vf across the capacitors can be calculated using:
Vf=QtotalCeq=−6×10−4C10×10−6F=−60V
Thus, the potential difference across them is 60V.
Step 5: Calculate the initial energy stored in each capacitor
The energy U stored in a capacitor is given by:
U=12CV2
Calculating for the first capacitor:
U1=12×4×10−6F×(150V)2=12×4×10−6×22500=0.045J
Calculating for the second capacitor:
U2=12×6×10−6F×(200V)2=12×6×10−6×40000=0.12J
Step 6: Calculate the total initial energy
Uinitial=U1+U2=0.045J+0.12J=0.165J
Step 7: Calculate the final energy stored in the combined system
Using the final voltage:
Uf=12CeqV2f=12×10×10−6F×(60V)2=12×10×10−6×3600=0.018J
Step 8: Calculate the heat produced
The heat produced Q is the difference in initial and final energy:
Q=Uinitial−Uf=0.165J−0.018J=0.147J
Final Results
- The potential difference across the capacitors is 60V.
- The heat produced is 0.147J.
The charge Q on a capacitor is given by the formula:
Q=C×V
For the first capacitor C1=4μF charged to V1=150V:
Q1=C1×V1=4×10−6F×150V=6×10−4C
Q2=C2×V2=6×10−6F×200V=1.2×10−3C
When the two capacitors are connected together, the total charge Qtotal is:
Qtotal=Q1−Q2=6×10−4C−1.2×10−3C=−6×10−4C
(Note: The negative sign indicates that the second capacitor has more charge than the first.)
The equivalent capacitance Ceq when capacitors are connected in parallel is:
Ceq=C1+C2=4μF+6μF=10μF=10×10−6F
The final voltage Vf across the capacitors can be calculated using:
Vf=QtotalCeq=−6×10−4C10×10−6F=−60V
Thus, the potential difference across them is 60V.
The energy U stored in a capacitor is given by:
U=12CV2
Calculating for the first capacitor:
U1=12×4×10−6F×(150V)2=12×4×10−6×22500=0.045J
U2=12×6×10−6F×(200V)2=12×6×10−6×40000=0.12J
Uinitial=U1+U2=0.045J+0.12J=0.165J
Using the final voltage:
Uf=12CeqV2f=12×10×10−6F×(60V)2=12×10×10−6×3600=0.018J
The heat produced Q is the difference in initial and final energy:
Q=Uinitial−Uf=0.165J−0.018J=0.147J
- The potential difference across the capacitors is 60V.
- The heat produced is 0.147J.
Topper's Solved these Questions
Similar Questions
A capacitor of capacitance 4μF is charged to 80V and another capacitor of capacitance 6μF is charged to 30V are connected to each other using zero resistance wires such that the positive plate of one capacitor is connected to the positive plate of the other. The energy lost by the 4μF capacitor in the process in X∗10−4J. Find the value of X.
View SolutionA capacitor of capacitance 4μF is charged to 80V and another capacitor of capacitance 6μF is charged to 30V are connected to each other using zero resistance wires such that the positive plate of one capacitor is connected to the positive plate of the other. The energy lost by the 4μF capacitor in the process in X∗10−4J. Find the value of X.
View SolutionFind charge on each capacitor and potential difference across each capacitor .

View SolutionA capacitor of 20μF charged upto 500 V is connected in parallel with another capacitor of 10μF, which is charged upto 200 V. the common potential is
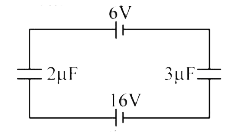
View SolutionWhat is the potential difference across 2μF capacitor in the circuit shown?
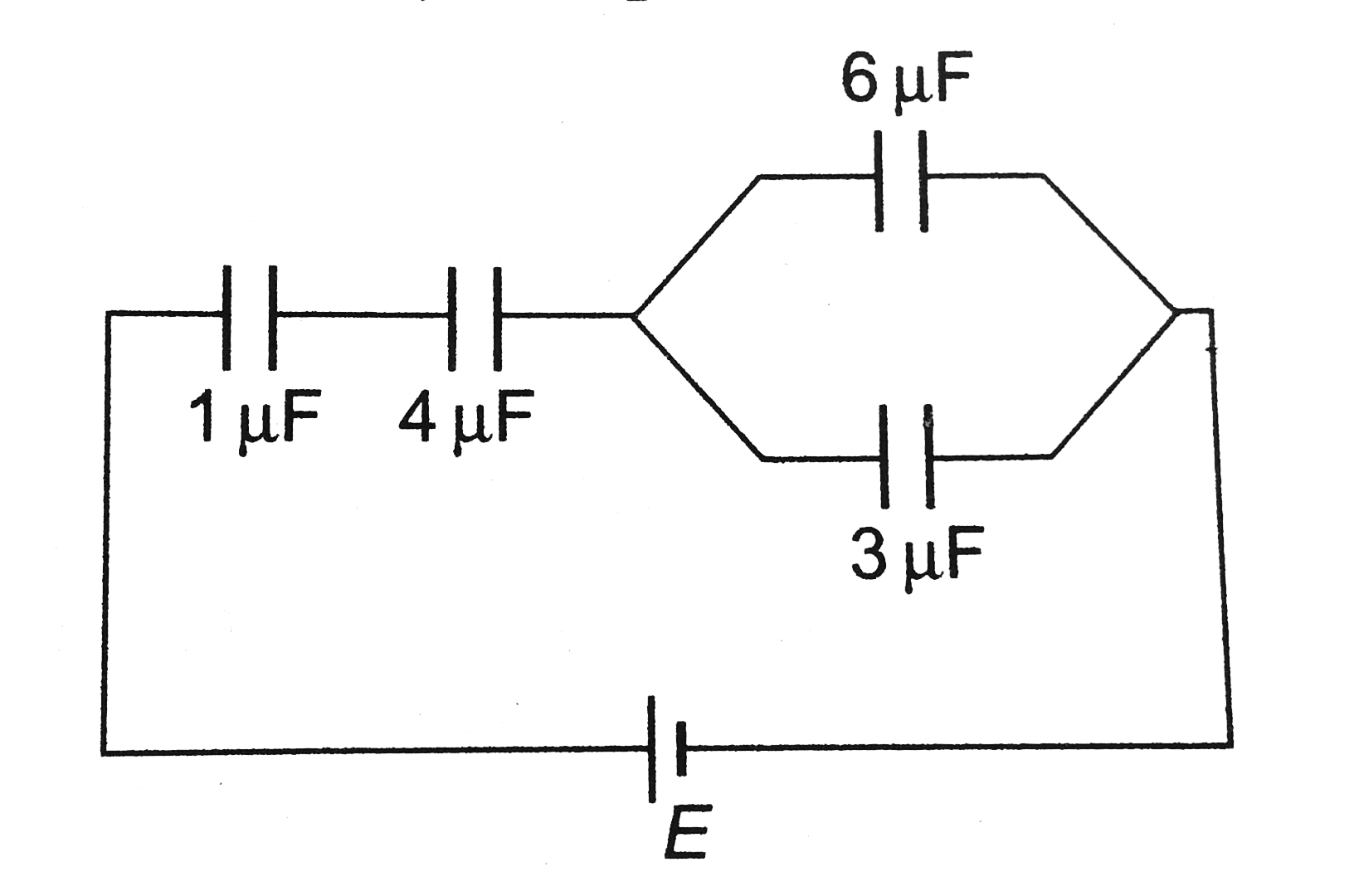
View Solutiongiven that potential differene across 1μF capacitor is 10V. Then,
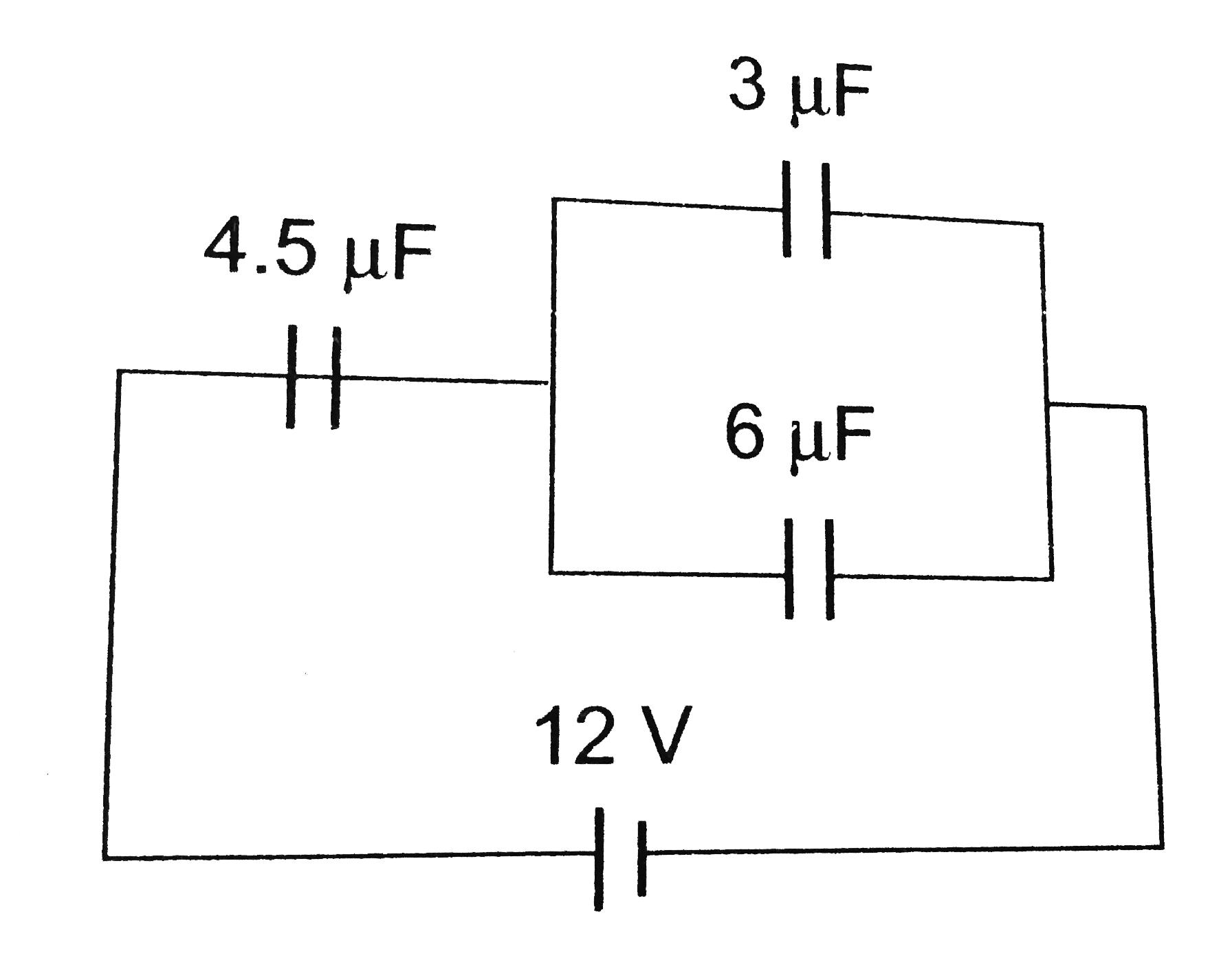
View SolutionIn the circuit shown in the figure, the potential difference across the 4.5μF capacitor is
View SolutionA capacitorn of 2μF charged to 50 V is connected in parallel with another capacitor of 1μF charged to 20 V. The common potential and loss of energy will be
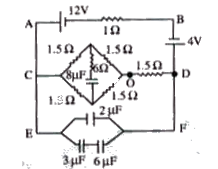
View SolutionIn the given circuit, the potential difference across the 6μF capacitor in steady state is
View SolutionIn the adjoning figure, the potential difference across the 4.5μF capacitor is

View Solution