A rocket of mass M is launched vertically from the surface of the earth with an initial speed V=√gR2 . Assuming the radius of the earth to be R and negligible air resistance, the maximum height attained by the rocket above the surface of the earth is RX where X is:
The correct Answer is:3
To solve the problem of finding the maximum height attained by a rocket launched from the Earth's surface, we will use the principle of conservation of mechanical energy.
1. Identify the Given Values:
- Initial speed of the rocket, V=√gR2
- Radius of the Earth, R
- Mass of the rocket, M (not required for calculations)
- Gravitational acceleration at the surface of the Earth, g
2. Write the Conservation of Energy Equation:
The total mechanical energy at the launch point (initial) is equal to the total mechanical energy at the maximum height (final). Thus, we can write:
Ui+Ki=Uf+Kf
Where:
- Ui = Initial potential energy
- Ki = Initial kinetic energy
- Uf = Final potential energy at maximum height
- Kf = Final kinetic energy at maximum height (which is 0 at maximum height)
3. Calculate Initial Potential and Kinetic Energy:
- Initial potential energy Ui=−GMmR
- Initial kinetic energy Ki=12MV2=12M(gR2)=MgR4
4. Calculate Final Potential Energy:
At maximum height H, the distance from the center of the Earth is R+H:
Uf=−GMmR+H
5. Set Up the Energy Conservation Equation:
Substituting the energies into the conservation equation:
−GMmR+MgR4=−GMmR+H
6. Simplify the Equation:
Rearranging gives:
−GMmR+H=−GMmR+MgR4
Dividing through by GMm (assuming M≠0):
−1R+H=−1R+gR4GM
7. Substituting g:
We know g=GMR2, so substituting gives:
−1R+H=−1R+R4R2=−1R+14R
Simplifying further:
−1R+H=−44R+14R=−34R
8. Cross-Multiplying:
Cross-multiplying gives:
4R=3(R+H)
Expanding and simplifying:
4R=3R+3H⟹R=3H⟹H=R3
9. Expressing in Terms of X:
The problem states that the maximum height H is given as RX. Thus:
R3=RX⟹X=3
Final Answer:
The value of X is 3.
- Initial speed of the rocket, V=√gR2
- Radius of the Earth, R
- Mass of the rocket, M (not required for calculations)
- Gravitational acceleration at the surface of the Earth, g
The total mechanical energy at the launch point (initial) is equal to the total mechanical energy at the maximum height (final). Thus, we can write:
Ui+Ki=Uf+Kf
Where:
- Ui = Initial potential energy
- Ki = Initial kinetic energy
- Uf = Final potential energy at maximum height
- Kf = Final kinetic energy at maximum height (which is 0 at maximum height)
- Initial potential energy Ui=−GMmR
- Initial kinetic energy Ki=12MV2=12M(gR2)=MgR4
At maximum height H, the distance from the center of the Earth is R+H:
Uf=−GMmR+H
Substituting the energies into the conservation equation:
−GMmR+MgR4=−GMmR+H
Rearranging gives:
−GMmR+H=−GMmR+MgR4
Dividing through by GMm (assuming M≠0):
−1R+H=−1R+gR4GM
We know g=GMR2, so substituting gives:
−1R+H=−1R+R4R2=−1R+14R
Simplifying further:
−1R+H=−44R+14R=−34R
Cross-multiplying gives:
4R=3(R+H)
Expanding and simplifying:
4R=3R+3H⟹R=3H⟹H=R3
The problem states that the maximum height H is given as RX. Thus:
R3=RX⟹X=3
The value of X is 3.
Topper's Solved these Questions
Similar Questions
A rocket is launched vertical from the surface of the earth of radius R with an initial speed v. If atmospheric resistance is neglected, then maximum height attained by the rocket is
View SolutionA body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View Solution
Knowledge Check
A rocket is launched vertically from the surface of earth with an initial velocity v. How far above the surface of earth it will go? Neglect the air resistance.
AREv2gRE−v2BREv2gRE+v2CREv22gRE−v2DREv22gRE+v2
A body is thrown from the surface of the earth with velocity (gRe)/12, where Re is the radius of the earth at some angle from the vertical. If the maximum height reached by the body is Re/4, then the angle of projection with the vertical is
View SolutionAssume that a frictionless tunnel is made in the earth along its diameter, a particle in projected in the tunnel from the surface of the earth with an initial speed v0=√gR, where g is the acceleration due to gravity on the earth's surface & R is the radius of the earth, if time taken by the particle to reach the centre of the earth is πn√4Rg the value of n is?
View SolutionA body is projected vertically upwards from the surface of earth with a velocity equal to half the escape velocity. If R be the radius of earth, maximum height attained by the body from the surface of earth is Rn. Find the value of n.
View SolutionA particle is projected vertically upwards the surface of the earth (radius Re) with a speed equal to one fourth of escape velocity what is the maximum height attained by it from the surface of the earth?
View SolutionA rocket is launched upward from the earth surface whose velocity time graph shown in figure. Then maximum height attained by the rocket is :
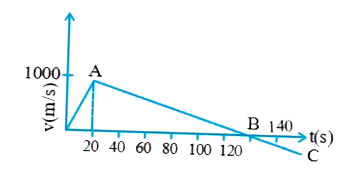
View SolutionA particle is projected vertically with speed V from the surface of the earth . Maximum height attained by the particle , in term of the radius of earth R,V and g is ( V < escape velocity , g is the acceleration due to gravity on the surface of the earth )
View SolutionIf a body of mass m is raised to height 2 R from the earths surface, then the change in potential energy of the body is (R is the radius of earth)
View Solution
